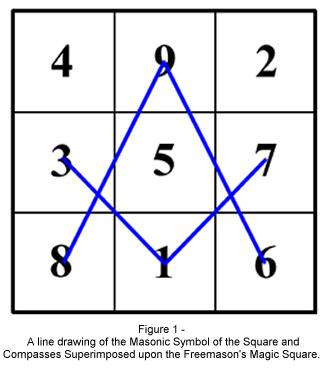
Some time ago I published a series of articles[i] in which it was speculated that the Masonic Symbol of the Square and Compasses may be a Sigil constructed using the Freemasons Magic Square. The Freemason’s Magic Square is one specific numerical arrangement of the several possible numerical arrangements of the ancient Magic Square of Saturn. It is the premise of these articles that the Square and Compasses symbol neatly fits the three-by-three grid (Figure 1) which comprises the Freemason’s Magic Square and that by using simple cryptographic techniques such as Alphabet/Number substitution (employing for example the Pythagorean Chart), some previously encrypted message may be revealed.

My purpose for this (the current) article however is not to further acquaint the reader with the Freemason’s Magic Square or to report the findings of my ongoing research pertaining to the Square’s possible use or origin as a Sigil. Instead I intend to present a different sort of analysis by considering the Square and Compasses as a purely geometric figure constructed within the three-by-three matrix of the Freemason’s Magic Square. I believe the results will be interesting to the reader.

Note that I am fully aware that there is absolutely no historical or factual basis supporting that this layout of our beloved Symbol is correct; none-the-less, this exercise does as a minimum lend itself to being a good lesson in mathematics and geometry. I trust that any controversy which arises from my musings on this subject will be tempered by this fact.  In this article I will present a second construction of the Square and Compasses which results in identical geometric characteristics. I do not suggest that the second construction supports my contention of the origin or use of the Square and Compasses as a Sigil. I do suggest however that the double square resulting from the construction of a Vesica Pisces and which results in line segments having lengths equal to the square root of 5, and the square root of two, is  common to both figures.

In the course of my analysis, I will be making certain assumptions which include that the reader understands basic principles of geometric construction, the nature of geometric proofs, and the concept of Divine Proportion[ii] (the Golden Mean or Phi). Where there is the possibility that the reader may be unacquainted with the more obscure geometric concepts which I mention, I have added extensive references where-by he may find basic explanations or further information.

The Square and Compasses

            The design of the Masonic Symbol of the Square and Compasses varies significantly. No single “official” design is known to exist, even though the Square and Compasses symbol has been copyrighted[iii]. In some instances the Compasses are depicted as having a forty-five degree included angle between the tips, and in other depictions the Square and Compasses are shown with a much narrower or broader span. Since I began this discussion with reference to the three-by-three matrix provided by the Freemason’s Magic Square, this matrix will be the basis for the layout of the Square and Compasses which I will pursue.

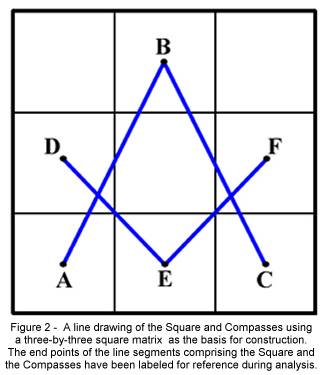
            Figure 2 below presents a three-by-three square matrix within which I have constructed a line drawing of the Square and Compasses. Since this is a geometrical analysis, I have labeled the three end points which describe the compasses as A, B, and C and have labeled the end points of the lines which describe the square as D, E, and F. Using this convention then, the compasses are formed by line segments A-B and B-C, while the square is represented by line segments D-E and E-F.

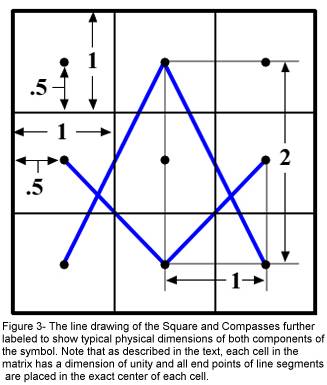
Assume that each square (cell) in the matrix has a dimension of unity. Therefore each cell in the matrix is a one-by-one unit square. Note that the ends of the line segments in the figure begin and terminate in the center of the cells comprising the matrix, with the result that ends of each line in the figure are positioned exactly one-half unit from the border of the larger square formed by the aggregate of the individual matrix cells . Figure 3 illustrates this along with the dimensions for the horizontal and vertical line components of the Symbol

Using this arrangement the angular dimensions of the “legs” of the compasses may be derived using the Pythagorean Theorem (The 47^th Proposition of Euclid) as follows:

            Pythagorean Theorem: c² = a² + b²

            Therefore,                               c² = 1² + 2²

            And,                                       c² = 1 + 4

            And it follows,                         c² = 5

            Resulting in:                             c= 5

It follows that the length of both “legs” of the Compasses (line segments A-B and B-C) are equal to the square root of five. The same derivation may be used to calculate the length of the “legs” of the Square:

            Pythagorean Theorem: c² = a² + b²

            Therefore,                               c² = 1² + 1²

            And,                                       c² = 1 + 1

            And it follows,                         c² = 2

            Resulting in:                             c= 2

Consequently, the lengths of the “legs” of the Square (line segments D-E and E-F) are equal to the square root of two. The reader will no doubt note that the square root of two is exactly the length of the diagonal of a true unit square.

Note also in our analysis that the symbol of the Square and Compasses exhibits perfect bilateral symmetry, and that each side of the symbol (left and right of the center vertical line comprising the matrix) may be enclosed in a separate double square. This is significant because the double square[iv] is the starting point for the construction of the Divine Proportion[v].

Divine Proportion

A straight (dashed) line may now be constructed which joins the endpoints (points D and F) of the square (Figure 4).  This line intersects the legs of the compasses at their respective midpoints and also intersects the vertical lines of the matrix at these same points. We will label the points of intersection, Point “G” and Point “H”.

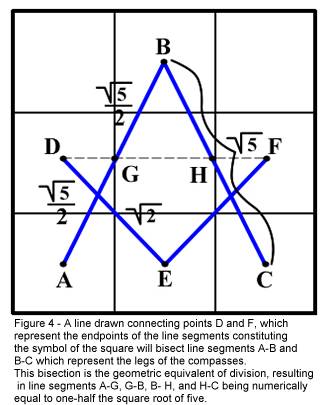
Since line segments A-B and B-C have been bisected, line segments A-G, G-B, B-H, and H-C now are equal to one-half the square root of five. This is important because the mathematical value of one-half the square root of five is exactly one-half less than the Divine Proportion, Phi. In other words by adding one-half (0.500) to the value of one-half the square root of five (approximately 1.118034) we obtain Phi, (1.618034). The golden ratio is also called extreme and mean ratio. According to Euclid[vi], a straight line is said to have been cut in extreme and mean ratio when as the whole line is to the greater segment, so is the greater to the less. This may be mathematically derived as follows:

In a line divided in accordance with the definition of Euclid, let the lesser part = 1, and the greater part = .

Then by the definition of the golden ratio[vii],

 / 1 = (1 +  ) / 

Therefore,

 ² = 1² + 1

Which, yields the quadratic equation,

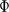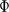 ² - - 1 = 0

Solving this quadratic equation for the golden ratio 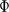 results in:

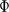= 1/2 + 5 / 2  1.618

 In our construction we are now presented with the opportunity to extend a straight horizontal line (Figure 5) from Point A to Point I, creating line segment A-I with a length of exactly one-half unit. If we were to swing an arc with a radius of A-I from Point A to a point (Figure 5 Point J) in alignment with line segment A-B, we would have effectively performed a geometric addition of one-half to the length of line A-B. In so doing we would have produced line segment G-J, having a length equal to the Divine Proportion (Golden Mean).

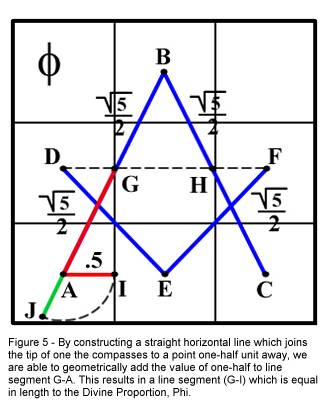
            It may further be seen from Figure 5 that line segment G-I also then has a total length of Phi.

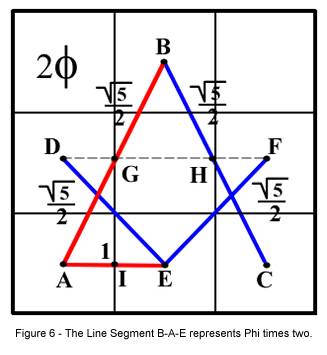
 In Figure 6 we have expanded this concept by extending line segment G-I to Point E, a distance of an additional one-half unit (Line A-E is one unit in length). The total length of line segment B-E then is two times Phi.

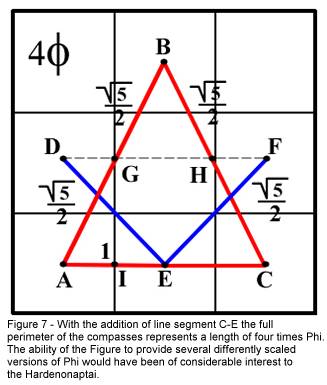
            Further extensions may be made to obtain line segments three times and four times (Figure 7) the value of Phi in length. In one of the following sections of this article we discuss the “Rope Stretchers”. This property of this figure might have been of particular interest to this group.

            Up to this point we have essentially ignored the geometric properties of the square other than its geometric function as a bisector of the compasses. Rest assured however that the square as constructed in our Figure also has unique geometric properties related to the value of Phi. In Figure 8, a version of the Square and Compasses is presented in which all except the basic references to the Compasses have been eliminated.

            In this figure, the classic method[viii] for dividing a line into mean and extreme ratio has been employed. An arc having radius E-F has been constructed from point F, which intersects line segment D-F (the hypotenuse of triangle D-E-F) at point G. Another arc of length D-G is then constructed from point D which intersects Line D-E at point L. In this construction, the ratio of the length of Line segment L-E to line segment D-L is equal to Phi. It follows that the same is true of the ratio of line segment E-F to line segment F-M. Note the precision with which the intersecting point of the Square and Compasses bisects the legs of the compasses while simultaneously dividing the legs of the square into mean and extreme ratio.

An Alternate Construction

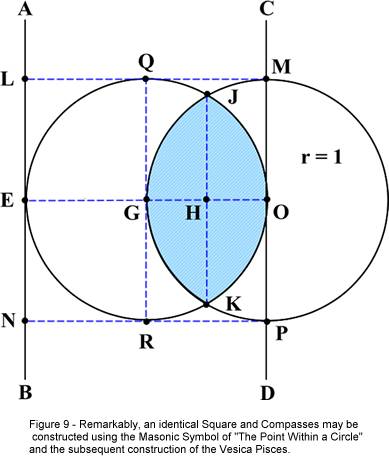
            As discussed, an alternative construction of the Square and Compasses may be performed in which the Divine Proportion is produced using the identical elements of the Square and Compasses. In this construction our starting point is the Masonic Symbol of “The Point Within a Circle” which has been altered by the addition of a second circle to produce the Vesica Pisces[ix] (Figure 9). Both circles in our Figure have a radius of one unit. I have labeled the Figure in a manner that will assist the reader in following the development of the construction.

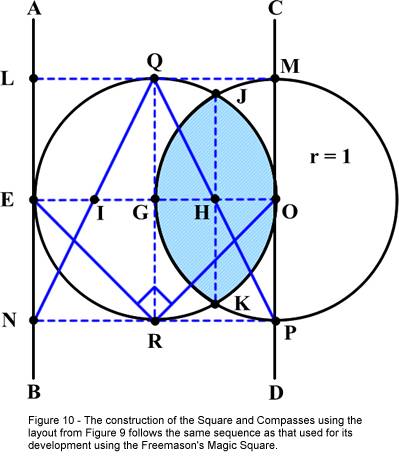
            In Figure 10, a line drawing of the Square and Compasses has been added. Note that the dimensions of the Square and Compasses are consistent with the dimensions used in the original construction. This is because both constructions rely upon the creation of a double square.

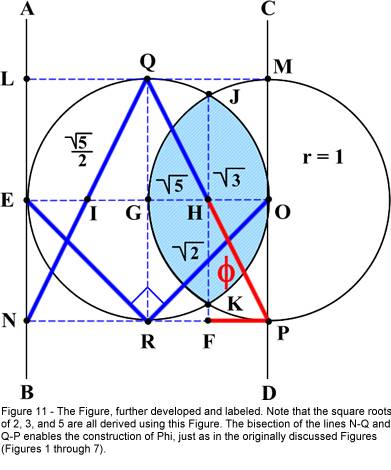
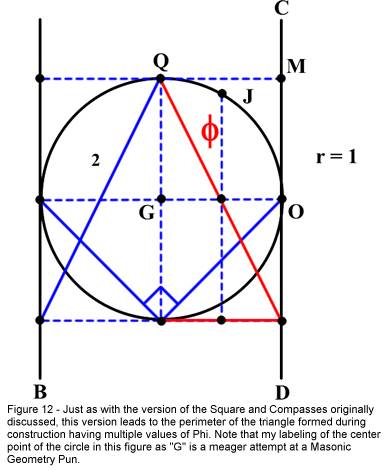
            In Figure 11, the construction has been further developed to illustrate that the value of Phi may be realized in a fashion identical to that utilized in the original construction. Figure 12 is the completion of the construction illustrating the creation of two times Phi. It follows that the construction is capable of producing Phi and three multiples of Phi (one time, two times, three times, and four times Phi). I chose not to repeat the development of Phi in the Square, which would be identical to that shown in the original Figure.

Rope Stretchers

            “Rope Stretchers” is the English translation[x] of the Egyptian word “Hardenonaptai”. It refers to the ancient engineers or surveyors who were believed to be responsible for the layout and measurement of monuments. This task was accomplished using ropes which had been knotted to mark specific dimensions or measurement reference points. In addition to ropes knotted to produce subdivisions of units such as eighths, quarters, halves, etc. the Rope Stretchers used ropes knotted to produce Pythagorean Triples. A rope containing twelve equally spaced knots[xi], for example, could be used to construct a 3, 4, 5 triangle, which is the basic triangle used for proof of the 47^th Proposition of Euclid. Diagrams of figures used by the Rope Stretchers to accurately knot ropes producing various equal graduations and the Pythagorean triples have survived to modern times as has an interesting ancient Egyptian sculpture believed to portray the Rope Stretchers [xii].

            It is also probable that the Rope Stretchers had knowledge of Divine Proportion[xiii]. Recalling our use of the square and compasses figure to construct a line having a value equal to one-half the square root of five, imagine the ease with which a rope could be knotted to this dimension, and the further ease with which an additional knot could be added exactly one-half unit in additional length. Naturally the laws of proportion apply for our figure, and consequently a rope knotted at the apex (pivot point) of the compasses, extended to the tips, and terminated with a knot at the “corner” (right angle) of the square would also represent the Divine Proportion. A complete circuit of the Compasses would provide either a large scaled version of Phi, or a rope having a length of four times Phi.

Conclusion

            If indeed the Masonic Symbol of the Square and Compasses symbol was intended to contain subtle references to Sacred Geometry[xiv], it is obvious that when the Symbol is drawn in the proportions shown here that references to Divine Proportion are present in abundance.