|
The 47th Proposition of Euclid and the
Masonic symbol of “The Point Within A Circle” are important in the Craft as
symbols of philosophical premise, and are fundamental in that capacity to an
understanding of Freemasonry. The Craft is rich in such symbolism, and yet we
often fail to recognize that beyond the allegory there often resides greater
light in the form of Geometry. The purpose of this paper is not to detract from
the metaphoric value of our symbols, but rather to expand the understanding that
these symbols, which are in large part based upon regular geometric shapes and
which may be constructed using the working tools of the craft. It is the view of
the author that many of Freemasonry’s symbols may be used much like
intermeshing gears, to arrive at implicit truths and illumination on a level of
understanding which cannot be communicated using spoken or written language
alone (much like music). Indeed, this feature may be by design a mechanism by
which future generations may achieve understanding of Masonic principles in
spite of changes in the context of language or inevitable changes in ritual. I
therefore present an exploration of how four such symbols, the 47th
Proposition of Euclid, “The Point Within A Circle”, The Vesica Pisces, and
The Divine Proportion are intricately related from the standpoint of Geometry.
Divine Proportion
The Divine Proportion has
recently received a great deal of attention by virtue of its inclusion in a
popular novel penned by Dan Brown. Novels aside, the Divine Proportion,
also referred to variously as the Golden Proportion, the Golden Mean, or simply
as Phi (f) is an interesting Geometric concept, and the fact that it occurs in
nature with astounding regularity makes it even more intriguing. History is
somewhat fuzzy concerning man’s discovery of the Divine Proportion and his
comprehension of its significance. One interesting version of history attributes
its discovery to Theano[i],
the wife of Pythagoras who inherited the role held by her husband as leader of
the Pythagorean mystery school following his death. Other versions insist that
the Divine Proportion was understood by man and incorporated into his
architectural works many centuries before this.
I will not belabor the
many instances in which the Divine Proportion manifests itself in creation[ii],[iii]
but will instead discuss its basic concept and its mathematical derivation as a
prelude to my discussions of the Vesica Pisces, which is closely associated with
the Geometric construction of Phi.
The
Divine Proportion refers to a certain proportional relationship between the
length of two lines which results when that line is divided into its mean and
extreme ratio (i.e. when the
ratio of the short part to the long part is the same as the long part to the
whole[iv]).
The actual value of the Divine Proportion (f) is a certain instance of an
incommensurate number, said to be irrational[v].
The exact numerical value of irrational numbers such as the square root of three,
Pi, and Phi cannot
be determined because their calculation creates an infinite series of non –
repetitive digits. They are, in effect, numbers of infinite dimension, which
none-the-less manifest themselves in reality.
The closest approximation for the value of Phi is nominally 1.618, or
more exactly expressed is 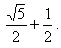
A derivation of the value of Phi
follows:

In
the above line AC, assume that line segment AB = f, and that line segment BC = 1
If
AB/BC=AC/AB, then B is said to divide AC in the extreme and mean ratio and is
equal to Phi ( f); and it follows that:
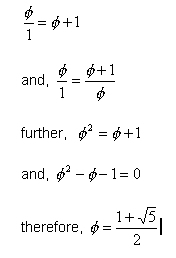
I will provide an
argument for the significance of the Divine Proportion in Freemasonry in later
portions of this paper.
The Point Within A
Circle
The point within a circle has largely been regarded strictly as a
metaphor within Freemasonry, and these metaphoric interpretations of the symbol
are both powerful and poignant. There are also a number of cases in which the
approach to understanding the symbol has been based purely upon its geometric[vi],[vii]
properties. This article intends to add to this body of work by proposing that
“The Point Within A Circle” as a geometric construction provides the pathway
for greater understanding of the Craft, and that it is an intricate part of the
Craft symbolism which works in concert with other symbolism to advance
understanding and provide more light. I will not provide great detail concerning
the appearance or construction of “The Point Within A Circle” as knowledge
of this is inherent in both Masonic Ritual and Masonic Literature.
Euclid’s 47th
Proposition
The 47th Proposition of Euclid, as with “The Point Within A
Circle” should require little introduction to the reader. Of all of the
Masonic symbols, this one tends to be that which has the fewest symbolic
interpretations[viii]. Although the utility of the 47th
Proposition is undeniable, we seem to often be at a loss for explaining its
allegorical or metaphoric relationship within the context of Freemasonry. In
Anderson's “Constitutions” published in 1723, it mentions[ix]
that the 47th Proposition of Euclid's first Book, which, if duly observed, is
the Foundation of all Masonry, sacred, civil, and military…”. In our ritual
the 47th Proposition is presented as a concept which teaches
Masons to be general lovers of the arts and sciences; however unlike the other
symbols to which we are introduced, no attempt at metaphor is made. I suspect
that the somewhat cold and hard technical nature of the 47th
Proposition makes it very difficult to consider it to be anything other than an
obvious utility. However, I believe that the 47th Proposition does
indeed have metaphoric content as a symbol and tool by which other greater
truths may be divined. It is in this context that I present the 47th
Proposition here.
The Vesica Pisces
The history of the Vesica Pisces is lost in the mists of time. Doubtless
this symbol existed during the time period ascribed to the life of Jesus Christ,
as this symbol was used as a covert means of identification for Christians. The
Vesica Pisces was used extensively during the middle ages, as may be evidenced
by its incorporation in the Gothic architecture of Cathedrals of that era[x].
Many readers will recognize that the Geometry of the Vesica Pisces and
its derivation, the Golden Rectangle play a prominent role in the layout of the
lodge room. I will not expound upon the symbolic or metaphoric meanings
attributed to the Vesica Pisces, which have been exhaustively covered in the
Literature. I will however deal with the Geometric properties inherent in the
construction of the symbol, and will use the Vesica Pisces in conjunction with
the other symbols of Freemasonry already described to illustrate the close
inter-relationship which they enjoy.
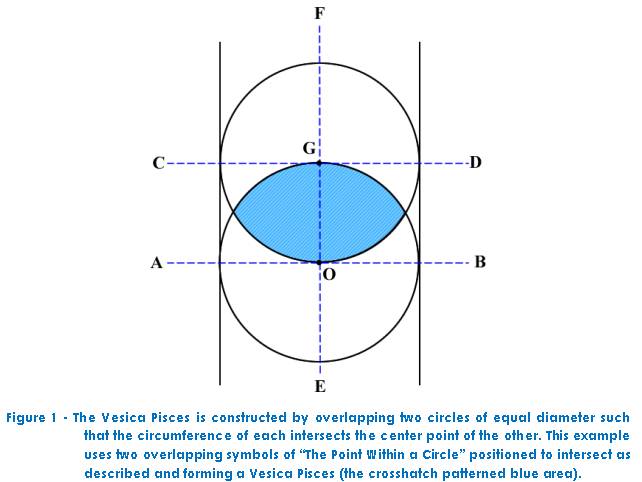
The Vesica Pisces may be constructed by overlapping two circles such that
the center of each circle lies upon the circumference of the other. In Figure 1
I have produced the Vesica Pisces by overlapping two separate constructions of
“The Point Within A Circle” (less the often included VSL or the images of
the two Saints John). The lozenge which forms the Vesica Pisces is highlighted
for clarity in blue cross-hatch. Both the horizontal (“A-B” and “C-D”)
and vertical (“E-F”) lines in the figure place the circle centers at Points
“G” and “O” respectively.
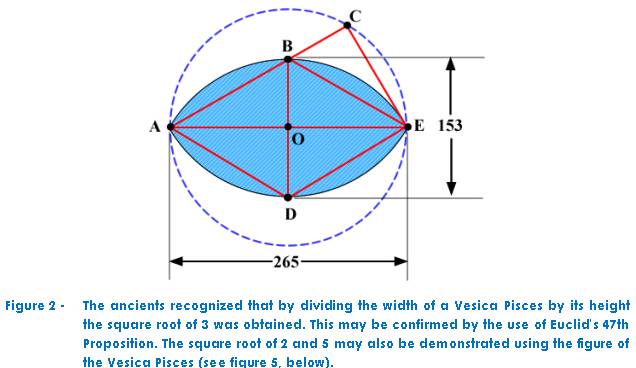
The Vesica Pisces itself has an
unusual mathematical property, namely that the ratio of the width to the height
of the figure when measured, closely approximates the value of the square root
of three (265 divided by 153). Figure 2 illustrates this feature. Figure 2 also
illustrates that the Vesica may be used to construct two perfect equilateral
triangles “ABD” and “BDE”. If the side of one of the triangles is equal
to unity (1) then the altitude of that triangle will equal the square root of
three. Note also that the side of either triangle (i.e. “A-B”) may be
extended through its point of intersection with the short axis (i.e. Point
“B”) to form a right triangle (“BCE”). This construction is based upon
Thales Theorem, and it produces five identical right triangles and a trapezoid
which contains them. This construction may be used as a proof figure for
Euclid’s 47th Proposition.
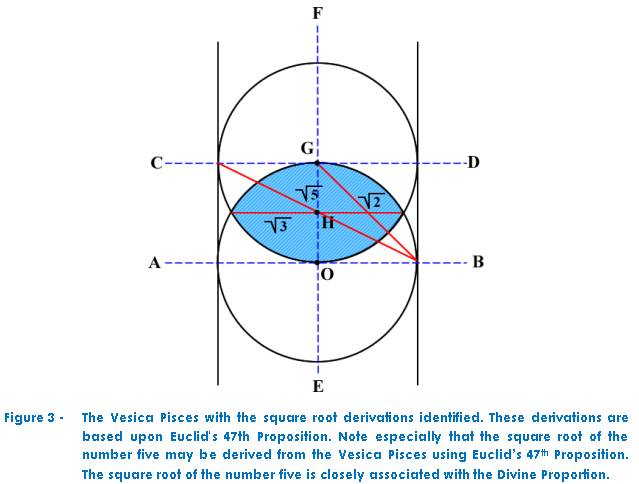
The Vesica Pisces may also be
used as a basis for the derivation of the square root of 2 and the square root
of 5 (See Figure 3). As discussed previously the value of the Divine Proportion
is very closely associated with the square root of five.
Derivation of the
Divine Proportion
Using the Vesica Pisces as a
foundation, it is possible to derive the Divine Proportion using the basic
techniques of Geometry. To illustrate this (Figure 4) we begin with a Vesica
Pisces upon which a right triangle has been constructed. You will note by
comparing Figures 4 and 5 that side “I-J” of
triangle “IJK” has a value equal to the square root of five.
Mathematically this may be derived by the use of Euclid’s 47th
Proposition since side “J-K” has dimension of one, and side “K-I” has a
dimension of two (one squared plus two squared equals five, therefore side
“J-I” equals the square root of five).
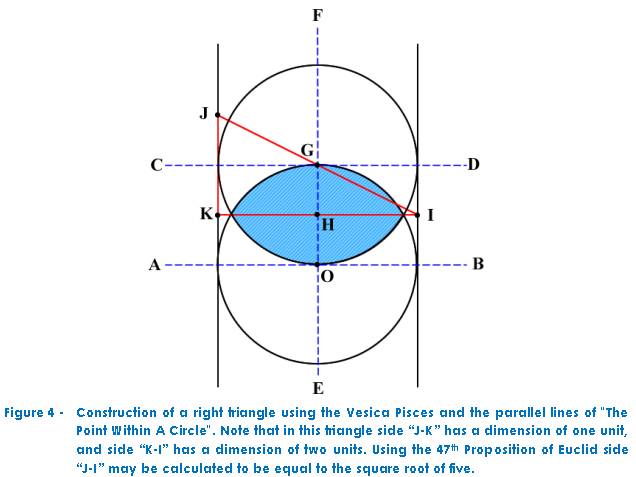
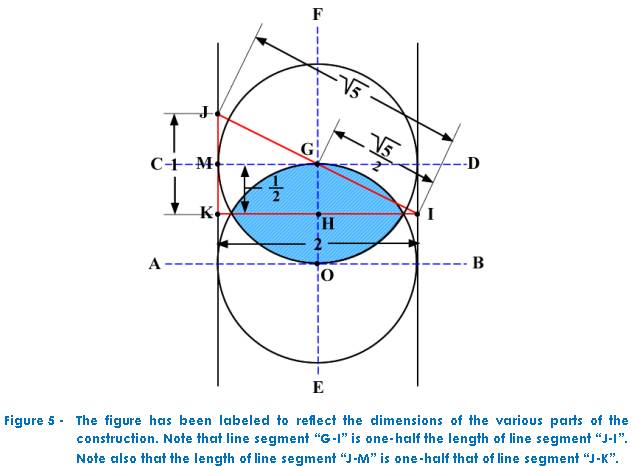
Figure 5 further illustrates
this case, and has been labeled to include the dimensional relationships found
in this construction. Of special interest in this figure are the dimensions
obtained by the division of triangle “IJK” by the vertical centerline
“E-F” to obtain triangle “IHG”. Note
that this triangle has a hypotenuse equal to the square root of five divided by
two, and that “G-O” equals one, the altitude of the triangle (“G-H”) has
a value equal to one-half.
Through a simple maneuver
(Figure 6) we may increase the length of the hypotenuse of triangle “IHG” by
exactly one-half by swinging an arc having a radius of “G-H” from point
“G” to a point at which the arc intersects the hypotenuse of triangle
“IJK” (Point “L” on Line “I-J”). This is essentially a form
of geometric addition in which we have increased the length of line segment
“I-G” (which is the square root of five divided by two) by exactly one-half.
This of course creates line segment “I-L” which has a length equal to Phi,
the Divine Proportion.

The Vesica Pisces as
illustrated here for the construction of the Divine Proportion is merely the
beginning of a wide number of applications for which geometric figures and
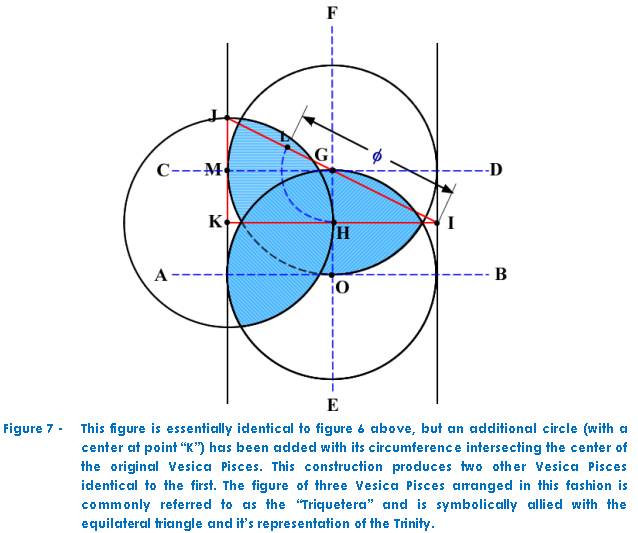
constructions involving the Vesica Pisces may be explored[xi]. Figure
7 is an example of this, in which an additional circle has been added to our
construction such that its circumference intersects the center of the original
Vesica Pisces. The result is the creation of two new Vesicas identical to the
first. The arrangement of three Vesica Pisces as shown in Figure 7 is called the
Triquetera, and is itself an ancient symbol of significance.
The question of the
significance of the Divine proportion and the Vesica Pisces naturally arises
from the preceding discussion. One published work[xii]
describes the implicit relationship of the Divine Proportion and Plato’s
Second Principle, known as the Indefinite Dyad, sometimes called the Greater and
the Lesser. This work emphasizes that Philosophers have pondered the concept of
Divine Proportion, perhaps long before it was known by this name. What they may
have learned, and what I believe the underlying significance of the Divine
Proportion and Vesica Pisces may be, is that there is an order in the universe
which surpasses man’s ability to quantify, and that this order is the source
of beauty.
In reviewing Plato’s Second Principle, I could not help but be struck
by the similarities between Plato’s understanding of reality and our emerging
understanding of Quantum mechanics. Man’s ability to glimpse the mind of the
GATU may be finite; however evidence of the infinite in creation improves our
understanding of his design.
[iii]
Colemaan, Michael. The Golden Ratio or Golden Section in Art, Science,
and Religion. http://www.miqel.com/fractals_math_patterns/visual-math-phi-golden.html
[vii]
Bowe, William F. A Certain Point Within a Circle, The Builder
Magazine, vol. 4, no. 7 (Jul. 1918), S. Brent Morris, The Hidden Secrets
of a Master Mason: A Speculation on Unrecognized Operative Secrets in Modern
Masonic Ritual. The Philalethes, vol. 36, no. 2 (April 1983)
[ix]
Meij, H. (Master Harmony Lodge No. 18). The 47th Problem of
Euclid. Freemason Information. Greg Stewart (Ed.)
[x]
Lawlor, Robert. Sacred
Geometry: Philosophy and Practice (Art and Imagination) Hudson
(March 1989) ISBN-10:
0500810303; ISBN-13:
978-0500810309
[xi]
Rachel
Fletcher: Musings on the Vesica
Pisces. Nexus Network Journal (ISSN 1590-5869), vol. 6 no. 2 (Autumn
2004).
|
![]() News Feed |
News Feed |  Subscribe News by Email
Subscribe News by Email