Numbers appear with astounding regularity in Masonic Ritual and within nature. It was the revelation that numbers may be used to describe and even predict phenomena found in the physical universe which prompted the Pythagoreans to develop their system of Theosophical Numerology. It is believed that Freemasons later incorporated significant portions of this Theosophy into Masonic ritual and practice; thus it is no surprise that numbers are so prominent in the Craft.

 Dealing with numbers sometimes requires an understanding of mathematics; however this understanding need not be advanced or even complex. This is true when examining our Rites and Symbols for evidence of hidden (numerically encoded) mathematical meaning.

While preparing a paper on the 47^th Problem of Euclid[i], my research unearthed an interesting fact concerning the numbers 3, 5, and 7 as are used in the Fellowcraft Degree to describe a certain spiral stairway. Specifically, the root or source of these numbers is derived[ii] by subtracting the squares of the first four integers (1, 2, 3, and 4) from one another in reverse order.

Figure 2 illustrates the process by which the sequential subtraction of the squares of 1, 2, 3, and 4 produces the numbers 3, 5, and 7.  Prior to this revelation I viewed the 3, 5, 7 sequence as being a simple progression of n + 2, in which “n” initially is the number 1 and by subsequent addition become 1 + 2 = 3, the resulting 3 becomes 3 + 2 = 5, and the resulting 5 becomes 5 + 2 = 7.  Logically then the next number in the sequence is 9.

It is the premise of this paper that the root method for the derivation of the numbers 3, 5, and 7 contains encoded within itself the Pythagorean Theorem. I intend to offer a mathematical proof of this hypothesis using the simple Pythagorean Triplet set 3, 4, and 5, which is of course the Triplet set used by Euclid in his figure of proof for the 47^th Proposition (Figure 1).

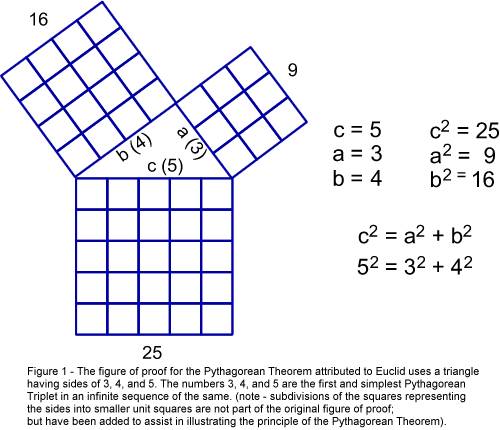
Basis for the Proof

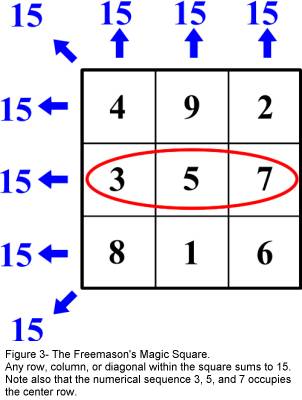
            When examining Figure 2, the reader will note that I have added one additional integer (the number 5) to the sequence of integers and squares. This addition is the logical extension of this numerical sequence of the first four integers, and is consistent both mathematically with the subtraction of the first three squares, and in the numerological context of Pythagorean Theosophy. I might add that the sum of the integers 1 through 5 is 15, (1 + 2 + 3 + 4 + 5 = 15), also happens to be the sum of the rows, columns, and diagonals in the Freemasons Magic Square, which itself incorporates the numbers 3, 5, and 7 (Figure 3). The inclusion of this integer is of course central to my proof as described here; however a second, much more mathematically involved proof is also possible using just the integers (and squares of) 1, 2, 3, and 4. The addition of the integer “5” shortens the math and dramatically simplifies the proof.

            I will present the proof in mathematical form in the following paragraphs. I have added notation wherever clarification appears to be needed, and I believe that the reader will find the mathematics fairly straight-forward.

Pythagorean Theorem

c² = a² + b²      [eq. 1] and, (Using the Pythagorean Triplet 3, 4, 5)

c = 5                (Given)

b = 4                (Given)

a = 3                (Given)

Root of 3, 5, 7 (and 9)

1, 2, 3, 4, 5             (Integers 1 to 5) also: (1, 2, a, b, c)

1, 4, 9, 16, 25         (Integers 1 to 5 squared) also: (1, b, a² or “b + c”, b² or “a² + c”, c²), therefore:

25 – 16 = 9             (Given), so:

c² - b² = 9               (substituting “c²”  for 25 and  “b²” for 16), and:

c² = b² + 9              (rearranging), and:

c² = b² + 4+ 5         (changing “9” into the quantity (4 + 5), and:

c² = b² + b + c        (substituting the value of “b” for 4 and “c” for 5), therefore:

 c² = b² + b + c            [eq. 2]

9 - 4 = 5                (Given), so:

a² - 2² = 5            (substituting “a²” for 9), and:

a² - b = 5             (substituting the value of “b” for 4), and (rearranging)

a² = b + c            (substituting the value of “c” for 5), therefore:

a² = b + c             [eq. 3] 

Proof:

(Using [eq.2] and [eq.3] as simple simultaneous equations)

c² = b² + b + c      (Given) [eq. 2] and:

a² = b + c               (Given) [eq. 3]

c² = b² +a²            (from [eq. 3] substituting a² for the quantity (b + c), therefore:

c² = a² + b²           (rearranging) [eq. 1]

Conclusion

            The ability to derive the mathematical formula for what could arguably be considered the framework for Masonry using information inherent in another Masonic symbol or allusion may seem startling; however I am of the opinion that this is not unusual at all. The inter-connectedness of Masonic allegory ensures that our learning is consistent with our principles, regardless of the source of inspiration, even when verbal accounts of the original meaning have been lost. Great truths often reveal themselves in more than one way and in more than one medium.