The 47^th Problem of Euclid is indeed enigmatic; while it is ostensibly a proof of a key principle of Geometry, its esoteric characteristics, not its mathematical properties are the source of its Masonic significance. Unraveling the complex riddle of the 47^th Problem and understanding why it is regarded as a central tenet of Freemasonry properly begins with study of its history and its mathematical application.  The Ritual during which the 47^th Problem of Euclid is introduced, briefly addresses these issues[i]; however having touched fleetingly upon the fundamentals, Ritual goes no further and it is left to the Candidate to undertake further exploration (or not).  The puzzling brevity with which the 47^th Problem is discussed, given the accompanying emphasis placed upon its importance to the Craft, seems almost to be an invitation for the intellectually curious to explore further. Most Candidates however seem to assume that their acquaintance with The 47^th Problem gained during their early years of formal education provides them with a more than adequate knowledge of the 47^th Problem of Euclid, and that they have already satisfactorily mastered the concept . Few ever investigate any further. Figure 1 shows the diagram of proof and construction lines upon which the original 47^th Problem of Euclid is based.

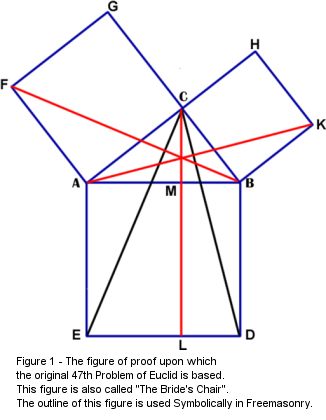To progress beyond the fundamental concepts and arrive at the door of understanding, preparatory study of the history and mathematics of the 47^th Problem is indeed essential; but ultimately one must discern that the true Masonic importance of the 47^th Problem lies not in its mathematical utility (which is considerable), but in the fact that the 47^th Problem as put forth by Euclid, is intended to apply to a very specific case of a right triangle having sides with lengths in   the specific proportions of 3, 4, and 5.

This paper is intended to serve as a bridge to an improved understanding of the Masonic meaning of The 47^th Problem of Euclid. Consequently it will include a very brief discussion of what is known about its history and a brief discussion of its mathematical basis. More significantly a discussion of the esoteric properties of the 3, 4, 5 triangle will then follow. I believe that at the conclusion, the reader will agree that there is more to The 47^th Problem of Euclid than meets the eye, and that much of the overtly mathematical associations of the 47^th Problem serve to intentionally veil its true (covert) meaning.

A Brief History

The actual formula c² = a² + b² for which The 47^th Problem of Euclid serves as proof actually predates[ii] Euclid (circa 300 BC) by more than 280 years. Pythagoras of Samos (circa 580 BC) is generally credited with its development.  There is Archeological evidence however that the Babylonians (1900-1600 BC) were familiar with the formula[iii] 1200 to 1400 years before Pythagoras. This evidence, established by a Babylonian artifact known as Plimpton 322[iv], consists of tables inscribed with “Pythagorean Triples” (Figure 2), groups of three integers[v] which may be used to construct perfect right triangles and which are an exact fit for the Pythagorean formula.

Pythagoras[vi] was an adept of Babylonian, Eleusinian, Greek, Egyptian, and Indian mystery schools.  The attitudes and beliefs of the Pythagorean Sect which he founded doubtless reflected those traditions. It’s also crucial to know that during the latter part of the 17^th Century AD, a major European revival of Pythagorean and other Gnostic philosophy took place. This time period corresponds to the period during which Freemasonry was emerging.

It is very important to view the symbolism of the 47^th Problem of Euclid within the context of the belief system of the Pythagoreans who are credited with its development. Aristotle[vii] in Metaphysica tells us that the Pythagorean mystery school held numbers and reason in the very highest regard. In fact, the Pythagoreans were the first to apply the didactic method to an examination of the universe and the GAOTU. A summary of the beliefs of the Pythagoreans might be that the presence of obvious design or purposeful intention is direct evidence of the GAOTU. Einstein said this best in his quip that “The existence of the watch is evidence of the Watchmaker”.  The belief of the Pythagoreans that the universe is ordered by the GAOTU in a mathematically precise manner was adopted by and incorporated into Freemasonry, resulting in conflict with the Church[viii] (Enclyclical of Pope Pius IX, Qui Pluribus, 9 November 1846); this in spite of the fact that The Song of Solomon (Book of Wisdom Chapter XI, Verse 20) proclaims “thou hast arranged all things by measure and number, and weight”[ix].

Numerology was one of the basic methods employed by the Pythagoreans (and by the Hebrews). The belief behind numerology is that numbers have mystical properties and associations. Numerology plays an important part in Freemasonry as well, especially as it applies to our rituals and symbolism. Very rarely however, are the details behind our numerological processes overtly revealed. My favorite example of this relates to the numbers 3, 5, and 7 which are prominent in the description of the “Winding Stairway” of the Fellowcraft Degree. If we square the first four integers, 1, 2, 3, and 4 and then subtract the square of each of these integers (1, 4, 9, and 16) from the square of the integer which follows it, we obtain the numbers 3, 5, and 7 (4 – 1 =3, 9 – 4 = 5, and 16 – 9 = 7). We will address numerology further in later portions of this paper. Be aware however that numerology and numerological techniques were considered useful tools to the Pythagoreans. Again, the Pythagoreans believed everything in the universe could be represented by numbers, and that nature was a vast arithmetical process. The GAOTU created everything to be in numerical harmony.

As an interesting aside, the figure of proof associated with the 47^th Problem of Euclid is known by many other names[x], including “The Brides Chair”, “The Francicans Cowl”, “The Peacock Tail”, “The Windmill”, “The Mousetrap”, “Euclid’s Pants” (my personal favorite), and “Dulcarnon”[xi] (meaning “to be at wits end” - the first book of Euclid is called “Dulcarnon”). The first English translation of all thirteen Volumes of Euclid’s Elements wasn’t published until 1606 by Sir Henry Billingsley (1606 AD). John Dee (renown Magus and Astrologer to Queen Elizabeth I) provided the preface for this edition[xii].  The first publication of the 11^th book in this edition of Euclid’s Elements contained paper “POP-UP” inserts of three dimensional models of the proofs.

Mathematical Properties

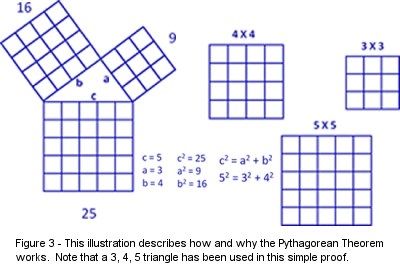
The basis for the mathematics of the Pythagorean Theorem and the Figure of Proof provided by Euclid can best be explained by considering three squares having dimensions of 3 X 3, 4 X 4, and 5 X 5 (Figure 3). For clarity, the squares shown in Figure 3 have been divided into unit squares of 1 X 1.

We can arrange these three squares so that their sides form a 3, 4, 5 triangle.  The area of each of the three squares can be calculated by multiplying the length of the side of each square by itself.  Therefore the area of the 3 X 3 square is 9, the 4 X 4 square is 16, and the 5 X 5 square is 25. If we assign a letter to each of the sides, so that the square with a side of 3 is a, that square with a side of 4 is b, and that square with a side of 5 is c we can relate the figure to the Pythagorean formula, c² = a² + b^2. . Since a = 3 then a² = 9, b = 4 and therefore b² = 16; and c = 5 so b² = 25. When we check the results we find that 25 = 9 + 16, and therefore c² = a² + b².

This explanation of the Pythagorean Theorem using the Figure of Proof from the 47^th Problem of Euclid is a very simple example of how the Figure of Euclid and Pythagorean formula are linked.  The actual proof given by Euclid is considerably more complex[xiii], but the result is the same. Several hundred detailed geometric proofs of the Pythagorean Theorem exist[xiv], including a famous one developed by U.S. President, Brother James Garfield.

Greek and Hebrew Symbolism

As stated earlier, the 47^th Problem of Euclid is not only a mathematical tool, it is also a symbol; in fact the mathematical utility of the 47^th Problem often (and I believe intentionally), veils the symbolic meaning, providing a sort of “smoke screen” intended to conceal that which is intended to be understood only by those willing to seek the underlying message (Let those with eyes see, and those with ears hear). I believe that there are two separate principles or messages which are revealed by the 47^th Problem of Euclid. Both however are tied to the fact that the 47^th Problem of Euclid (unlike the Pythagorean Theorem) uses a very specific case of a right triangle as its basis. This special case is that it employs a right triangle which has its sides in the exact proportions of 3, 4, and 5.

I would like to begin with the first veiled message, which incorporates the ancient principles of the Divine Trinity represented by the Masculine, the Feminine, and the Offspring. This concept is ancient in origin and was spoken of by Plato (Circa 348 BC) in Book VIII, Chapter III of The Republic[xv] in which he advances a description of the so-called “Nuptial Figure”, which is a triangle having sides in the proportion 3, 4, and 5.  Plato describes the perpendicular side as 3, the base side as 4, and the hypotenuse as 5.  He further states that the square of 5 is the sum of the squares of 3 and 4.  The description given by Plato of the Nuptial figure indicates that he was familiar with the Pythagorean formula. Plutarch (46 A.D.), in a later commentary, refers to Plato’s Nuptial Figure[xvi] and adds that based upon Plato’s description that the perpendicular represents the male, the base the female, and the hypotenuse the offspring.  This interpretation is founded upon the fact that the Pythagoreans and ancient Hebrews considered that 3 is the first odd, and therefore male number; 4 is the square of 2, the first even and therefore female number; and that 5 is the offspring of the two (3 + 2). Early Egyptian mystery schools[xvii] considered this linked to Isis, Osiris, and Horus. We, as modern Masons generally consider that this concept expresses the masculine and feminine characteristics of the GAOTU, merged in the offspring of the two. As previously described, numerology played an important role in the symbolic representations of the Pythagoreans, and this practice carries over into Freemasonry. As an example, the number 3 is prominent in Masonic ritual, as it is in the natural world. In Masonry there are three degrees; three principal officers; three original Grand Masters; three lesser lights; three great lights; three movable jewels’ three immovable jewels; three of fifteen who traveled in a westerly direction; three raps; three gates; three steps on the Master’s Carpets; three steps in Masonry; three supporting pillars. There are similar manifestations of the number three throughout nature. As we will discover, in the case of the 47^th Problem of Euclid the number 3 is extremely important in its symbolic meaning.

One of the techniques used in numerology, which is in fact central to the science, is that of numerical reduction[xviii]. Complex numbers are here considered to be any integer which has more than one digit. To properly analyze and understand numbers Numerologists employ a simple process to reduce complex numbers. It involves adding the digits of any complex number together (sometimes more than once) until a single digit results. In addition to two common examples of this process I have added the Reduction of Nines. 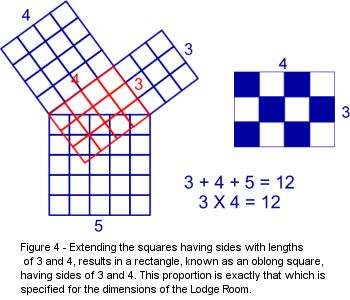The reduction of nines has no bearing upon our discussion of Euclid but was included because it is fun to observe that all the products of nine and any other number reduce to nine. In our Figure of proof given in The 47^th Problem of Euclid, it is significant that the sum of the length of the sides of the three squares equals 12.

If we ignore for a moment that square having a side of 5, it can be observed that an oblong (rectangle) can be projected (Figure 4) from the two remaining sides of our figure having the relative dimensions (proportions) of 3 X 4.  The area of this figure, obtained by multiplying 3 by 4 is 12. Of course in the numerological reduction of 12, we determine that 12 = 1 +2 = 3.

If we examine the prescription for the dimensions of a lodge room, as given by Mackey’s Masonic Encyclopedia, we find that a lodge should be an oblong square (we find further reference to the oblong square in Masonic Ritual) having dimensions such that it is 1/3 longer than it wide; in other words, a 3 X 4 rectangle, just like the one we obtain in our figure of proof by projecting the sides having lengths of 3 and 4 to produce an new rectangle.  The uncanny link to the 3, 4, 5 triangle and our lodge room becomes as they say, more and more mysterious when we consider that during circumambulation of the lodge[xix] (in some Masonic Jurisdictions) the EA circumambulates 3 times, the FC 4 times, and the MM 5 times. Circumambulation, by-the-way, involves making a complete circuit around the Lodge, while keeping the right hand toward the altar. Circumambulation is also called “Squaring the Lodge”, and the number of circumambulations is counted based upon the number of times in which the Northeast corner is reached. With the completion of one circumambulation, the candidate has traveled twice a distance of 4 (the length of the Lodge from West to East and East to West) and twice the distance of 3 (The length of the Lodge from North to South and South to North). This sums to a total distance of 4 + 3 + 4 + 3 = 14; and 14, reduced is 1 + 4 = 5 (the length of the diagonal distance across the lodge). Therefore, a Mason raised in this manner[xx], has reproduced by circumambulation the numbers three, four and five in the most significant corner of the Lodge[xxi] (the Northeast). When a Candidate kneels at the altar while binding himself to his obligations, he kneels at the center of the diagonal, a place representing birth. It might also be considered that the oblong square, which is two 3, 4, 5 triangles sharing a common diagonal, may express a reflective relationship between the celestial and the earthly, such as that embodied in the Hermetic theosophy that the earthly plane is a reflection of the Divine (“That which is above is like to that which is below, and that which is below is like to that which is above." - from The Corpus Hermeticum of Hermes Trismegistus[xxii]).

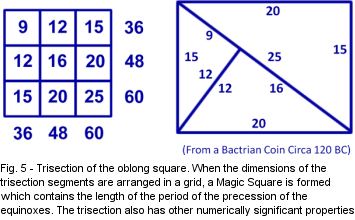There are further properties of the 3, 4, 5 triangle and the oblong square which may be revealed through numerology combined with the Geometric operation known as sectioning (or dividing). One well-known sectioning operation is the Trisection of an Oblong Square[xxiii] (Figure 5), in which the oblong square is divided into three similar triangles, each having sides with the proportions of 3, 4, and 5. Placing the dimensions of each triangle resulting from the trisection in a 3 X 3 grid results in a so called “Magic Square”. The sum total of the numbers comprising the magic square is 144 ( 12²) . Multiplying 36, 48, and 60 yields 103,680 which is 4 times the duration in years of one complete precession of the equinoxes (25,920 years). A similar operation called Quadrisection[xxiv] results in a Geometric derivation of the dimensions (in cubits) of the ancient measurement systems of the world, including the Greek Stadia and the Egyptian Khet.

Ancient Hebrew Scholars developed “Gematria”, their own system of numerology[xxv], which is based upon the fact that Hebrew letters were also used as numbers (think of Roman Numerals (I, V, X, L, C, M etc.). This concept, which is part of a system known as Kabbalah considers letters and words to have numerical equivalents, and that the numerical values of these words and letters have established meanings. Gematatria is one of three systems of Kabbalistic numerology (Temura and Notarikon being the other two).  One stunning example[xxvi] of the use of Gematria in the Pentateuch (or Torah) is that which analyzes the text involving Moses and the burning bush.

According to this analysis, “Moses in Hebrew is spelled with the three letters MEM-SHIN-HEH (Mosheh) which has a Gematria of 345, as follows: Mosheh = MEM (40) + SHIN (300) + HEH (5) = 345 . On the other hand, the Hebrew name by which God first announces Himself to Moses is Eheyeh Asher Eheyeh ("I Am") which has the following Gematria:  Eheyeh Asher Eheyeh = EHEYEH (21) + ASHER (501) + EHEYEH (21) = 543 . Thus Moses (with a Gematria of "345") is a reflection of God (with a Gematria of "543"). In other words, we see in the sequence 543/345 a "palindrome" in which Moses (345) emerges as a "reflection" of Yahweh (543)”. This “reflection” may also hold true in a much broader sense, as voiced in the Hermetic maxim “as it is above, so it is below”[xxvii]. This concept was addressed in earlier discussions pertaining to the oblong square.  The number 345 may also be directly interpreted as “God Almighty” (El Shaddai) or 1+30+300+4+10).

Astrological Symbolism

Euclid’s 47^th Problem also exhibits an astrological connection. Magic Squares are a hobby of mine (yes, I need to get a life). A magic square[xxviii] is an arrangement of numbers in a grid of squares such that the sum of the numbers along any column or across any diagonal are equal. Magic squares have existed for centuries and were frequently associated by Alchemists with the Planets[xxix]. A magic square was in fact referenced earlier in relation to the Trisection of an oblong square. Figure 6 shows the three magic squares associated with the planets Saturn, Jupiter, and Mars.

A Pythagorean Magic Square exists[xxx] (Figure 7) in which the sum of the diagonals, rows, and columns of all three squares comprising the figure of proof for The 47^th Problem of Euclid are equal to 174 and which, when reduced, have a numerological value of three ( 1 + 7 + 4 = 12 = 1 + 2 = 3). If we square the sum of the numbers in each square we find that it observes the Pythagorean formula. 

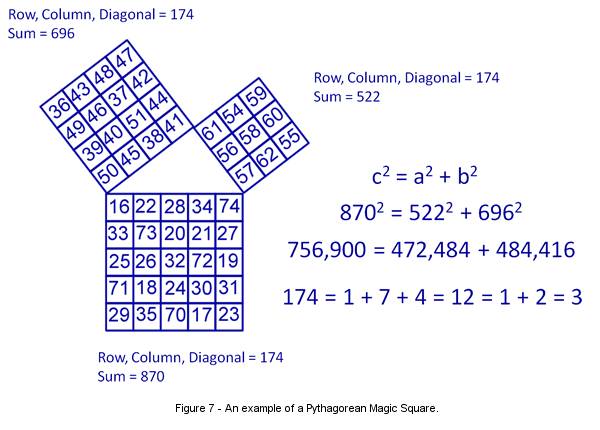
We also find in this figure that the cross-sectional area of the 3, 4, 5 triangle formed in the figure is 6 (3 X 4 = 12 and 12/2 = 6). This is significant because the number 6 is associated with the Sun. As mentioned, the introduction of the 47^th Problem of Euclid as a Masonic symbol occurred during the European revival of Pythagorean Philosophy during the 1700’s. This was also a period when men such as Galileo (1564 – 1642 AD) were being arrested and jailed for expressing the Heresy that the Sun and not the earth was the center of our solar system. The implication here is that the three prominent planets Saturn, Jupiter, and Mars are arranged in such a manner as to suggest that the Sun is at the center.

Conclusion

When considered in the context of ancient beliefs and philosophies, the 3, 4, 5 triangle which is an integral part of the 47^th Problem of Euclid has meanings and characteristics well beyond those commonly associated with its mathematical usage. One of these meanings is that the 3,4,5 triangle, which is central to the 47th Proposition represents the Philosophical Male, Female, and the union of the two (Offspring). This relationship is the basis for the Theosophy of the Trinity. When extended to the oblong square, consisting of two 3,4,5 triangles arranged to share a common diagonal, we find an allusion to Hermetic theosophy proclaiming that earth is a reflection of the Divine (as above, so below).

 A second meaning is that in which it is suggested that the Planets revolve about the Sun, and not the Earth, which during the middle ages would have been a great heresy. This meaning would certainly align with that portion of our Ritual which informs us that the 47^th Problem of Euclid teaches Masons to be “general lovers of the arts and sciences”.