“Thus it is no longer surprising that Man, imitating his Creator, has at last found a method of singing in harmony which was unknown to the ancients, so that he might play, that is to say, the perpetuity of the whole of cosmic time in some brief fraction of an hour, by the artificial concert of several voices, and taste up to a point the satisfaction of God his Maker in His works by a most delightful sense of pleasure felt in this imitator of God: Music.”

Johannes Kepler, Harmonices Mundi[i]

The Chartres Labyrinth holds a special interest for me. It is among other things, the first full scale labyrinth which I personally circumambulated. I should more correctly say that it was a full scale replica, and that it was located in a Presbyterian Church near Columbus, Ohio (which is a long way from France). I undertook this activity shortly after being raised as a MM and I remember at the time being fascinated with the intricate, almost mathematical pattern of the labyrinth. Following my experience, I began to research labyrinths in general and the Labyrinth of Chartres in particular. This research revealed that walking the Labyrinth is considered to be a symbolic journey from life to death[ii] and that in medieval times walking the labyrinth was accepted as a surrogate for a pilgrimage to the Holy Land[iii].  The Labyrinth is also believed to possibly be an ancient astronomical device or calendar.

In the course of my research I happened upon an article[iv] prepared by Eminent Freemason Bro. Bruno Gazo, Editor of Pietre-Stones Review of Freemasonry. This article deals with the concept of rhythm and unconscious (emotive) thought processes. Having, in the course of my analysis of the Labyrinth, discovered repetitive patterns embedded within the design, the realization occurred that these patterns could well be described as rhythms. Further reading[v] indicated labyrinths are widely regarded to have rhythmic characteristics. This paper discusses my examination of the rhythms of the Chartres Labyrinth and provides the basis for my analysis of the Labyrinth and its rhythmic properties.

The Labyrinth

During medieval times there was a very close link between the Craft Masons and the Knights Templar[vi].  The Templars sponsored the building of Cathedrals throughout Europe, and it makes perfect sense that in so doing that they employed, and enjoyed a cordial relationship with, large numbers of Craft Masons. One particular project which was sponsored by the Templars was the building of the great Cathedral in Chartres, France. This beautiful Gothic structure still stands, and is world famous for its art and architecture, including a large Labyrinth which graces the floor of the Cathedral nave.  In his excellent book, Masonic Symbols and Signposts[vii], Bro. Leon Zeldis does a wonderful job discussing Labyrinths and their connection to Freemasonry, and includes an excellent illustration showing the Chartres Labyrinth.

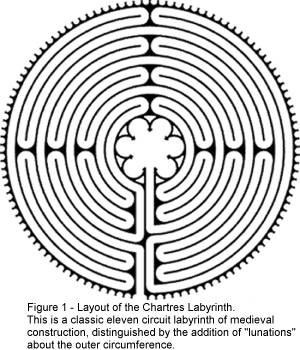
            The Chartres Labyrinth is a circular, stone mosaic construction[viii] (See Figure 1). It is an eleven circuit unicursal (one way in and one way out) design. The labyrinth is divided into four segments and the path to the center contains twenty-eight turns (seven per section, fourteen per side). The circumference of the labyrinth is bordered by 112 lunations, an average of twenty-eight lunations per section[ix]. I say “average” because the lunations are not uniformly distributed. One side of the labyrinth actually contains fifty-seven lunations, while the diametrically opposite side contains fifty-five[x]. This difference creates an inequality in spacing of the lunations. This inequality of spacing is not believed to be an anomaly but rather it figures into certain elliptical features of the lunar orbit. Note that the number 28 (28 = 4 X 7) appears frequently here. Many researchers have commented upon the calendar-like properties of the labyrinth. For example, the four segments containing 28 lunations each (on average) could perhaps represent four, 28 day long, months (after all a month averages four, seven day long weeks).

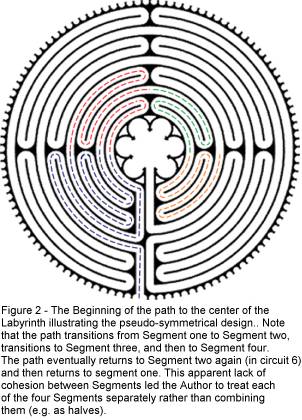
The Chartres Labyrinth itself is unique in that it presents an initial appearance of symmetry, with each segment and each half appearing to mirror the segment or half directly opposite. In fact the design is pseudo-symmetrical[xi], and each segment is unique. To illustrate this, I have traced the initial path of the Labyrinth leading to its center in Figure 2. Note that there is no true geometric symmetry in the design.  Interestingly, the Chartres Labyrinth, though circular can also be drawn in a square configuration[xii].

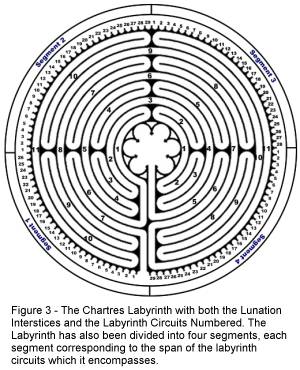
            As a preliminary to analyzing the Labyrinth, In Figure 3 I have modified the original (Figure 1) by sequentially numbering the interstices (spaces in between the spokes of the lunations) in each segment of the labyrinth and by similarly numbering each of the eleven circuits.  During my discussions of the labyrinth these numbers will be points of reference.

Figure 4 has been developed by tracing the path to the center of the labyrinth using a system in which the path through each segment is represented by a different color (segment 1 – blue, segment 2 – red, segment 3 – green, and segment 4 – orange). Additionally I have tracked the continuity of the path within each segment using a series of dashed and dotted lines.  I have considered continuity here to be the unbroken path within each segment bounded by the two points at which that path crosses from or into the next segment. I have used a light dashed line for the initial path in each segment, a bold dashed line for the second path, a dotted line for the third path. One segment (segment 3) contains a fourth path which I have designated using a combined dashed and dotted line.

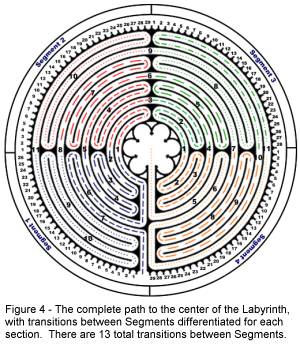
            Using a conventional twelve month calendar as a reference, each segment of the labyrinth would represent a quarter, with each quarter consisting of three months.  Each of the three continuous paths in a quarter (other than segment 3 which has 4 paths) would therefore represent one month.  While the math may be right for this calendar-like scenario, it is obvious from Figure 4 that things are a bit more complicated than that. Specifically the paths do not flow through the segments sequentially. A good example of this is path 4 in Segment 2 (Figure 4), which clearly flows “backwards” to Segment 1 instead of continuing to Segment 3 as a nice, well-behaved calendar might be expected to do. Clearly the segments do not represent quarters of the year as we would expect based upon modern calendar conventions.  Apparently the 13^th Century understanding of linear calendar time was different than the modern concept, or there is an alternative event other than time being represented here (my attempts to determine a correspondence between the Labyrinth and Planet retrograde motion have been unsuccessful).

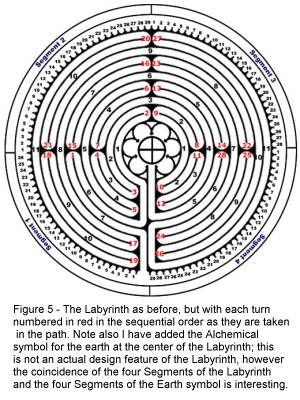
Figure 5 shows the labyrinth annotated so that each of the 28 turns in the labyrinth is labeled relative to the segment and circuit in which it occurs.  Table 1 provides the same information in tabular form where the display of the resulting pattern is more obvious.  In this table I have specified a turn as occurring at the point at which it ascends or descends to the next circuit. Additionally I have color coded the turns according to the segment in which they occur using the same color system used for the lines shown in Figure 4.

            Table 1 demonstrates that the 28 total turns in the labyrinth are completed in a pattern such that 7 turns in Segments 1 and 2 are addressed first, then 7 turns in Segments 3 and 4, whereupon the final 7 turns in Segments 1 and 2 are completed, followed by the completion of the 7 turns in Segments 3 and 4.  This pattern of path completions mimics lateral (mirror image) symmetry. The path to the center is reached by completing 4 paths from Segment 1, and 3 paths from Segment 2, followed by the same completion pattern in Segments 3 and Segment 4. The pattern moves to finish Segments 1 and 2 by the completion of the remaining 3 paths in Segment 1 and the remaining 4 paths in Segment 2, before following an identical pattern in the completion of Segments 3 and 4. In all cases the completion pattern is 2 – 2 - 3, except for the first two and last two paths which are sequential.

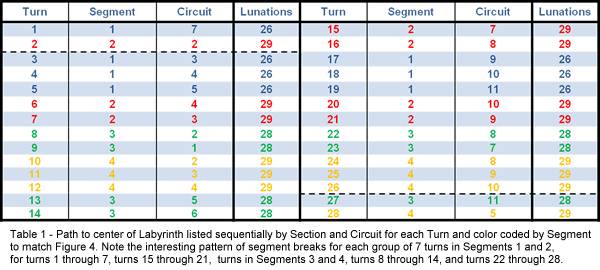
            This seems quite remarkable because without the uneven number of continuous paths resulting from the extra (i.e. the fourth) continuous path in Segment 3 (Circuit 11) this pattern would not be possible. Upon completing Table 1 it was evident that the various paths in the labyrinth could be represented as continuous rhythm by visualizing each path as a separate beat. This may be demonstrated by recording these beats using musical notation. Since we have no indication that any of the notes correspond to a specific tone (or pitch), we can treat them as a monotone rhythm, and represent them musically using standard musical symbols. Figure 6 provides the musical notation which describes the Labyrinth’s complex rhythm.

            For the benefit of non-musicians (I am one myself) I would recommend that to enhance your understanding of musical notation you may wish to visit the very informative website provided by Daniel Laberge[xiii], or the equally excellent website provided by “Number A Productions”[xiv].  I will dive into the murky waters of conjecture by offering the observation that each note in the rhythm of the Labyrinth could be assigned a tone based upon its position (from one to eleven) in the circuit in which it occurs. For example given nine normal positions for a note on the staff, and with two additional notes on a ledger line (perhaps one above and one below the staff) one might produce a harmony. A more detailed mathematical analysis by persons familiar with harmonics would possibly result in a different, but equally interesting interpretation.  Rhythm and harmony were very important to the Pythagoreans[xv] who believed that music and geometry were two of the four forms of mathematics (Astronomy and Arithmetic being the other two – together they form the Quadrivium[xvi]). Clearly the Pythagoreans understood the ability of rhythm, which is the basis of music, to affect us in a spiritual context.

            One aspect of the Labyrinth which I have not yet attempted to explore is the connection between rhythm and dance. Dance has historical ties to the Labyrinth of Chartres and many other Medieval Labyrinths[xvii]. The Chartres Labyrinth was reportedly circumambulated by monks using a peculiar “bat wing” dance step. This may be tied to the Crane Dance[xviii] allegedly introduced by Theseus of Crete, and said to represent the course of the sun. Theseus was of course famous for his Minotaur exploits in Greek mythology. There are also possible ties to certain Minoan rites of Phaistos and Knossos.  I suspect that the many changes in the directional progression of the Labyrinth may have some ecclesiastical significance.

Conclusion

            Visualize the rhythm of waves falling upon the seashore for just a moment. I suspect that this simple audio visualization will have elicited in you an overwhelming sense of tranquility.  Visualize the rhythm of the breath of someone you love as they lay sleeping. Rhythm has the power to invoke emotions. Consider the atmosphere of a crowded dance floor in which the dancers are moved to a frenzied pace- by rhythm. The universe is filled with rhythm, from the rising and setting of the Sun to the seasons of the year, to the beating of our own hearts. It’s no accident that Johannes Kepler[xix] referred to “the music of the spheres” when contemplating planetary orbits in “Harmonices Mundi” (The Science of the Harmony of the World).

I have not yet discovered how or whether the Labyrinth of Chartres represents an astronomical chart or a calendar of celestial events; however I know that these events occur in a rhythmic sequence and that the rhythm of the Labyrinth may very well prove to have celestial mechanics as its basis.