W. Bro Gest joined a Sussex based lodge in 1986 and was the Master in 1993. Since then, he has held almost every office in the lodge, and presented the 2nd degree TB continuously for 10 years. He received his Provincial honours in 2001, and in the same year, published a paper about the Sussex Masonic Centre which was the starting point that triggered writing the book The Secrets of Solomon’s Temple. He has delivered several talks to lodges in Sussex and London since 1995 on a diverse range of Masonic subjects, all based on his own original research and enquiry. His current role is as Charity Steward in his Lodge, and to fill a vacancy that occurred, is also Senior Warden – again. He is also a member of Royal Arch Chapter.

Well before the development of sophisticated arithmetic compilations, geometry was an important tool for solving the types of problems that today we solve easily as a consequence of our mathematical understanding. It was realised by our ancestors that three geometric figures -the square, circle and the triangle -formed the foundation of nearly all their particular problem solving. The circle was the most revered of all the geometric symbols, being a line which had no definable beginning and therefore no end, and as such represented infinity. The centre of the circle was the most revered point, being that from which every part of the circumference was equidistant, the centre of creation and therefore infinite in its power. In addition the easiest of the three symbols to construct was the circle. A peg could be hammered into the ground, a length of cord or material loosely tied to the stake at one end and a stick at the other, and then whilst holding the cord or material taut, one could scratch a circle in the ground by walking around the stake. However it was derived, the circumference of the circle could then be used to establish the four faces of a square.
 

THE INTERVIEW NOTHING IS WANTING BUT THE KEY. Bruno Gazzo interviews Kevin L. Gest about his book 'The Secrets of Solomon's Temple'

BG: Why has Solomon's Temple been so revered over the centuries? KG: Jedidiah's (Solomon's) Temple was a place of worship. It was also a celestial observatory and a centre of education, with the rooms reserved for the priests, which surrounded the main body of the Temple, being used as the centre for learning. It was a Holy Place because it reflected the true nature or God's creation and how wonderful that seemed as expressed through the pattern of the seasons, predictability of events, resultant geometry, clock and a calendar -a structure in total harmony with the macro-cosmos. It was a demonstration of technology. The pillars became a repository/record of celestial mechanics, plus geometry, which determined the principles on which the structure was designed. The science provided the influence on customs, regalia, social structure and,ultimately, on nationhood. The pillars were a unique encyclopaedia in stone and bronze, details of which were known to only a few -the dimensions and their significance were hidden from those who did not need to know -a secret and sacred repository of information. In Freemasonry there is an expression used and related to the pillars which states: :"for therein were deposited the constitutional scrolls". This sentence creates the impression of a cavity, a hole or a place in which scrolls or other works were hidden, information that was to be known to but a few. The key word, I believe, is therein, not therein as in some secret cavity but therein meaning within the dimensions of the pillars - the data about the Sun, Moon, precession and earth mechanics. This would not have been so different from the Egyptian practice where they engraved information on pillars and obelisks in hieroglyphics, as a record. BG What was the secret of Solomon's Wisdom? KG: The Wisdom of Solomon (Jedidiah) was his knowledge and application of the principles of geometry (mathematics) remembering that he sought wisdom (understanding and knowledge) enabling him to reach logical conclusions. He was an expert on flowers, trees and animals. The Old Testament text tells us that "he was more knowledgeable than the men of the East" which is possibly a reference to his understanding of astronomy/astrology (science). He sought this wisdom before he started building the Temple. He was educated in the principles of ancient wisdom. Reference to his lateral thinking abilities are, perhaps, really a more modem interpretation of what we define as wisdom. BG: What is the secret of Solomon's Seal? KG: I suggest that the geometric shape of the interlocking triangles is derived from the interlocking circles of Vesica Pisces which indicates an understanding of ancient/sacred geometry; that Vesica Piscis, being the basis of Solomon's Seal, is the key to the ground-plan and dimensions of the Temple. BG: Why is it called 'Solomon's Temple'? KG: I suggest that because of its special features the temple became known as the 'Temple of Sol and Amon'. Sol meaning Sun Amon meaning Moon. After his death, Jedidiah was referred to as the man who built the Sol and Amon Temple, which became corrupted over time to Sol-amon and then to Solomon. The pillar heights were the same but interpreted differently to reflect celestial information. For example, when the shaft is given the dimension of 18 cubits it reflects solar information, whilst when it is referred to as 17.5 cubits it makes allowance for 0.5 cubit to be covered over as a seating boss for the capitals and the resultant dimension reflects information relative to the Moon.It may even have been that the two pillars were different sizes, reflecting that 0.5 cubit difference and that Jachin to the South contained information about the Sun and Boaz to the north contained information about the Moon. In various parts of the United Kingdom, one can find displays of very old Masonic regalia. Thus it was that I noted a freemason's apron from the era 1751. In particular it shows the two pillars with an image of the Sun and Moon over each. It is as if this knowledge was well known in Freemasonry at some time in the not too distant past. BG: Do you think Solomon’s Temple was actually built in Jerusalem? KG: There is no conclusive archaeological evidence to prove that it was, or wasn’t. There have been three Jewish/Hebrew temples on the same site so it is not impossible that evidence has been covered or destroyed in building the second two temples. BG: Isn’t freemasonry just a load of mumbo jumbo anyway? KG: No. To those who are not members but have seen something on television, or read some of the derogatory books of yester-year, it may seems so. As I have conducted my own enquiries I have come to respect the ceremonies as part of process of education that ultimately led to one being acclaimed as a Master Mason – someone who was not only skilled with hand tools to carve stone, but a good designer, construction engineer, architect, a thinker – someone well versed in geometry and celestial mechanics. BG: I very much enjoyed reading your book, Secrets of Solomon’s Temple, thank you, and I found much of your analysis to be impressive and convincing.. Yet you may be wide of the mark on your interpretation of the name Solomon. I have found it to be Sulemain or Sulaiman, or Sulma sometimes Slr. Salma or slr is quoted as being the root of shalom=peace. What makes you think your interpretation is right? KG: Thank you for your comments about the temple. As for Solomon, I’ve read many works over the years by all manner of writers who claim he was all sorts of people, from Moses to Amenhotep III, and most of that is based on pure speculation. The text of the old testament has remained unchanged for over 2000 years, so I’ve stuck with the translated word that is shown there and the fact that when it was first translated into Latin it was with the alchemic terminology which suggests that the scribes of that time, had some very specific reason for attributing such a derivation. There is a logical link in the process.

The principles of geometry were recorded in a series of theorems expounded by the Greek mathematician Euclid around 300 BCE. One of the first principles he alludes to is a process of dividing a straight line into two equal parts. This is done by taking the line, AB, and drawing two circles of equal diameter, one circle at each end of the line, so that they overlap.

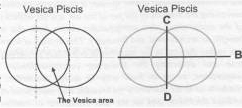
Drawing a vertical line between the points C & D will bisect the line AB into two equal lengths. This concept can be taken one stage further when the circles, both of equal diameter, are drawn such that the circumference of one circle touches the centre of the other circle. This geometric pattern was well known to the ancients and has been passed down to us with the title Vesica Piscis. The resultant area where the two circles overlap is known as the Vesica.

It produces some interesting characteristics. For example, it is possible from this use of the two circles to determine an angle of 30° and 60°. This is shown in the diagram below

This simple geometric structure immediately lends itself to the construction of another important figure -the equilateral triangle.

So, our ancestors, through their knowledge of geometry, were able to produce, with considerable accuracy, the three most common geometric forms in their construction armoury -the circle, the square and the equilateral triangle -the latter two being derived from the basic form -the circle. Thus, the circle became a highly regarded geometric device. But, more importantly, it was the point at the centre of the circle which was most revered, for no circle could be constructed without it.

And, as the circle became the form for the origins of so much other geometry, which in turn provided the basis for the construction of many of the temples, palaces and significant buildings of ancient times, so this point within the circle was seen as the centre from which all creation emanated. One can imagine how, through their knowledge of the interlinked macro-cosmos, and a belief that God had designed and implemented every last element of it himself, our ancestors believed that He must have used the same geometric principles. So, too, it can be imagined that the centre of the circle, infinite in the wisdom and knowledge that could be derived from it, was revered as God himself.

The vesica, or central area of the interlocked circles, was treated not only with reverence but as a sacred entity. It was an area from which so much else, geometrically, could be created. With their knowledge of the macro-cosmos, it was not lost on our ancestors that the shape was not dissimilar to that of the female vulva, the origins of intelligent form -the origins of all of us. It thus represented the geometry of life.

The book can be ordered at Lewis Masonic.

Read our Book-Review