The Geometric properties of mutually tangent circles have been studied for centuries by Geometers such as Apollonius of Perga in Greece (3^rd Century B.C.), Rene Descartes of France (circa 1643), Phillip Beecroft of England (1842), and Frederick Soddy in 1936 to name but a few[i]. 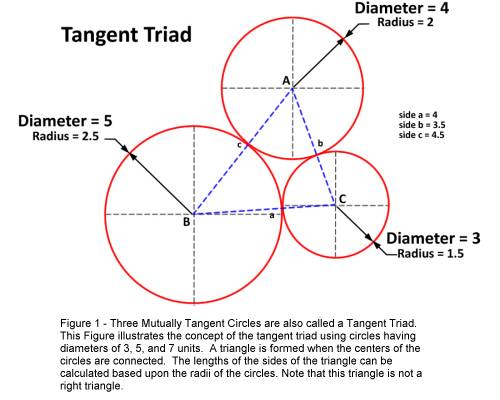Also called “Kissing Circles”, this geometric construction usually involves two or more circles which touch one another at only one point, the point of tangency. Figure 1 illustrates three mutually tangent circles. When three circles are arranged such that they are mutually tangent the resulting figure is called a Tangent Triad. Connecting the centers of a tangent triad forms a triangle (Triangle ABC in Figure 1).

Soddy, who received the Nobel Prize for Chemistry in 1921 was so taken with “kissing circles” that he penned a poem[ii] about them, which reads in part:

“For pairs of lips to kiss maybe

Involves no trigonometry.
'Tis not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.”

Figure 1 illustrates three mutually tangent circles having diameters of 3, 4, and 5 units, which have been constructed with their centers at the vertices of a triangle. Notice in this figure that the lengths of the sides of the triangle are the sum of the radii of the two circles which lie at the endpoints of the sides (the triangle vertices). Therefore we find side “b” to have a length equal to 3.5 units, side “a” has a length equal to 4 units, and side “c” a length equal to 4.5 units.

While pondering “Kissing Circles” one day (with regrettably less passion than Mr. Soddy) I began to wonder what I might find if I constructed three mutually tangent circles with their centers at the vertices of a Pythagorean Right Triangle having sides with lengths of 3, 4, and 5 units. I have often speculated that the Figure of Proof for the Pythagorean Theorem developed by Euclid is important to Freemasons not because of its intrinsic mathematical value but because it specifically makes use of a 3, 4, 5 right triangle. Historically, the 3, 4, 5 right triangle is believed to make allusion to the Trinity of Osiris, Isis, and Horus or to the principle of the divine masculine, divine feminine, and the union of the two.

What I discovered during this construction is quite interesting; whether or not it was actually Pythagoras who truly exclaimed “Eureka” upon discovery of the unique philosophical, mystic, and geometrical properties of the 3, 4, 5 right triangle, I believe that he was definitely onto something.

Construction of the Figure

            In my construction of the figure, I decided that the simplest approach was to work out the required dimensions and positions of the circles first, and to then overlay my 3, 4, 5 triangle upon the result. With a bit of math and reasoning, I determined that the diameters of my circles needed to be 2, 4, and 6 units and that each of the two larger circles needed to be positioned at right angles to the third, smaller circle. Naturally, the three circles would also need to be tangent to one another. Figure 2 below illustrates the result of my construction.

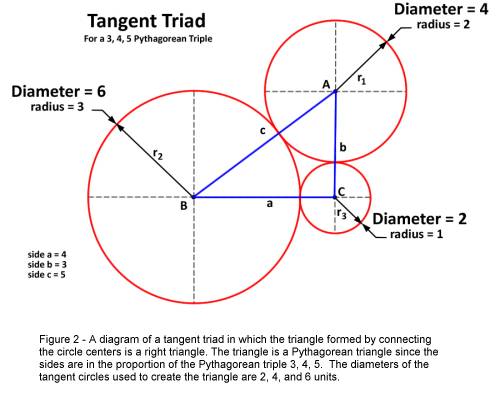
            I have connected the centers of each circle in Figure 2 to form a right triangle. Note that by adding the length of the radii of the two circles which comprise them, the lengths of the sides of the triangle may be determined. Mathematically speaking:

a = r₁ + r₂ = 1 + 3 = 4

b = r₁ + r₃ = 1 + 2 = 3

c = r₂ + r₃ = 3 + 2 = 5

            Notice also that the centers of Circle “C” and Circle “A” and (separately) of Circle “C” and Circle “B” are collinear and that the two pairs of circles are aligned ninety degrees to one another. Triangle “ABC” therefore is a 3, 4, 5 right triangle.

            I will note at the outset that one of the interesting characteristics of this construction lies in the fact that the perimeter of the triangle (3 + 4 + 5 = 12) and the sum of the diameters of the three circles used in my tangent triad (2 + 4 + 6 = 12) are identical.

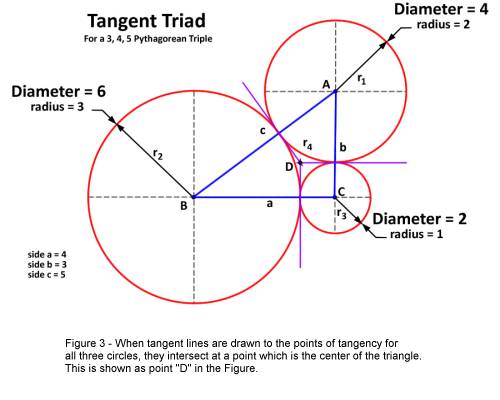
            With tangent triads (or any circles which are mutually tangent), lines (tangent lines) drawn through the points of tangency will all intersect at a point which is the center of the triangle. Figure 3 illustrates this. In Figure 3, Point “D” represents the intersection of tangent lines at the center of the triangle. The same point (Point “D”) may also be located by the intersection of three lines bisecting each of the angles of Triangle “ABC”.

            An additional feature which I discovered concerning this center point is that a circle (called an in-circle[iii]) inscribed in the 3, 4, 5 triangle, such that it is exactly tangent to all three sides of the triangle, will be exactly two units in diameter (the same as circle “C”).  This is illustrated by Figure 4, and can be confirmed by calculation of the in-circle radius using a standard formula[iv] as follows:

r₄ = [(a) (b)] / (a + b + c)

r₄ = [(3) (4)] / (3 + 4 + 5)

r₄ = 12 / 12 = 1

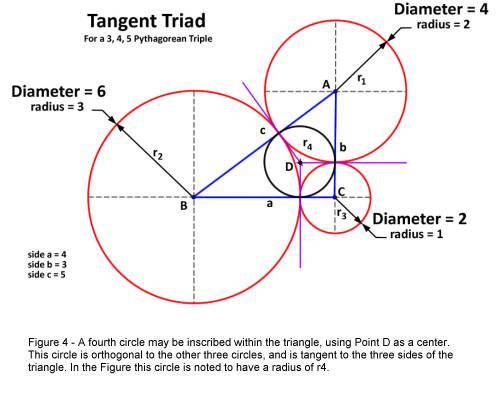
Therefore, with a radius of 1 unit, the diameter of Circle “D” is 2. In our Figure then, Circle “C” and Circle “D” are the same in diameter.

            For clarity, in Figure 5 I have constructed lines which are tangent to Circle “D” and to Circle “C”. The obvious result is that the Masonic Symbol (shown in black ink) of the “Point Within A Circle” appears.

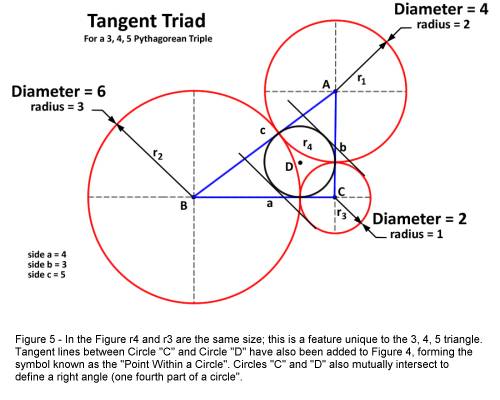
The only triangle which has an in-circle with a radius of 1 (a diameter of 2) is the 3, 4, 5 right triangle. When considering the relative positions of Circle “C” and Circle “D” in Figure 4, note that the two circles overlap such that they intersect one another at their circumferences to exactly define a right angle (one-fourth part of a circle).

I will leave it to the reader to marvel at the fact that at least three important Geometric constructions, which are closely identified with Freemasonry, may be derived from this single construction. From the standpoint of Pythagoras, I believe that geometric characteristics such as these would have further affirmed his belief in the divine nature of the 3, 4, 5 triangle.