Symbols were used by primitive man as the earliest form of writing. With many symbolic illustrations great care has been taken to embellish, decorate, and adorn the symbol; sometimes to clarify the symbolic meaning, and in others to disguise or obfuscate the symbolic content.  This paper explores two classic examples of symbolic illustrations which appear in Book Two, Chapter xxvii of Three Books of Occult Philosophy[i]^,[ii] by the noted 16^th Century Alchemist, Henry Cornelius Agrippa, entitled “Of the Proportion, Measure, and Harmony of Man’s Body”. These symbols are very complex geometric figures accompanied by obscure references to philosophical concepts. The exploration undertaken in this paper will specifically focus upon the geometric properties of the figures.

Agrippa’s Figures

The unique proportional relationships displayed by the human body appear to have been known in times of antiquity. Vitruvius (circa 30 B.C.) in Book III of his treatise De Architectura[iii] detailed these proportions in writing as follows:

“The navel is naturally placed in the centre of the human body, and, if in a man lying with his face upward, and his hands and feet extended, from his navel as the centre, a circle be described, it will touch his fingers and toes. It is not alone by a circle, that the human body is thus circumscribed, as may be seen by placing it within a square. For measuring from the feet to the crown of the head, and then across the arms fully extended, we find the latter measure equal to the former; so that lines at right angles to each other, enclosing the figure, will form a square”.

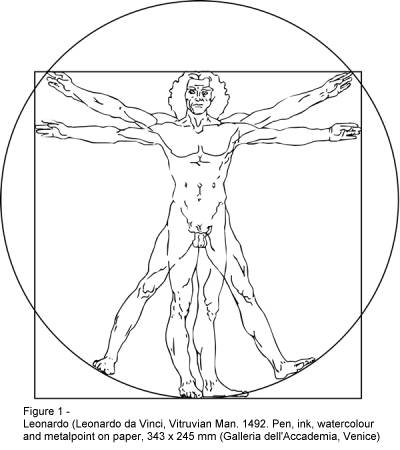
This description (circa 1487) was used by Leonardo DaVinci to create the famous drawing entitled Vitruvian Man (Figure 1)[iv]. Figures similar to Leonardo’s have been created over a very broad span of time (some earlier, some later) by Philosophers and Artists such as Hildegard von Bingen (1098-1179), Fra Giovanni Giocondo (1435-1515), Bartolommeo Caporali (1442-1509), Cessare Cesariano (1483-1543), Francesco di Georgio (1482-1489), Robert Fludd (1617), and Eliphas Levi (1810-1875).

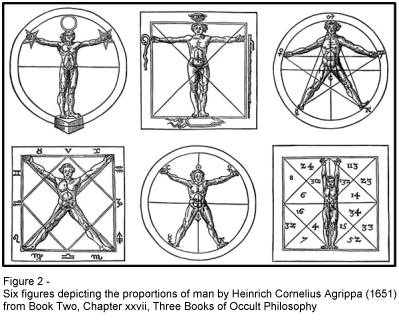
Agrippa was likely aware of many of these drawings when in 1651 he published his Three Books of Occult Philosophy. The six figures published by Agrippa in Book Two, Chapter xxvii are, at first glance, quite similar to Vitruvian Man (Figure 2 is a collage of these figures[v]). In these figures, Agrippa symbolically suggests, by enclosing man in a circle (itself the symbol of perfection and infinity) his (man’s) relationship to the divine or cosmic realm. Another of these figures illustrates the human form with outstretched arms (similar to Vitruvian Man) enclosed in a square, illustrating the "four square measure," where man "will make a quadrature equilateral"[vi].

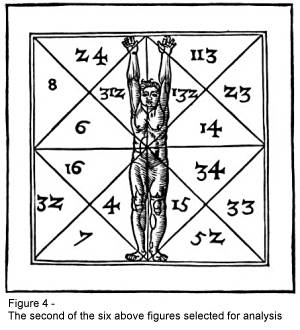
I have selected two of these six figures for analysis, and they are reproduced below as Figure 3 and Figure 4.  Please note that while the remainder of Agrippa’s figures in Chapter xxvii are also immensely interesting, these two share a common symbolic theme and have identical geometric properties. Limitations of space do not permit the other figures to be fully discussed or further developed, although they will be briefly considered in relation to the two figures of interest.

     

Geometric Properties

The geometric concepts represented by both Figure 3 and Figure 4 are essentially identical. In fact the analysis of these figures is best handled by treating them as a single composite figure, combining certain elements of each. Two unique characteristics of the figures are especially worth noting; First of all, the body position of the human form in Figure 3 is such that the arms and legs are aligned with the diagonal of the Square in which it appears. The body position of the form in Figure 4 on the other hand is aligned with the height dimension of the square. It is an important point to recognize that if the human form in Figure 3 is rotated about its center point (the navel) the hands and feet will trace a circle which neatly circumscribes the square. Also, in regard to the symbols of the zodiac as they appear in Figure 3, the reader will note that the zodiac typically is displayed in a circular format, corresponding to the celestial sphere. The fact that the symbols of the zodiac appear in the border as they do in this figure, fairly begs the viewer to visualize a circle inscribed within the outer square. Please also note that the symbols of the zodiac are also critical to an understanding of the figure’s philosophical interpretation.

In Figure 4, the hands and feet of the human form, when rotated in a similar fashion, will trace a circle which is exactly inscribed within the square. Figure 4 requires that for geometric analysis we temporarily ignore the numerical values which appear in each of the triangular sections of the drawing. Note that absent the human form, Figure 4 resembles Figure 3 except that two additional lines have been added perpendicular to one another and intersecting at the center.

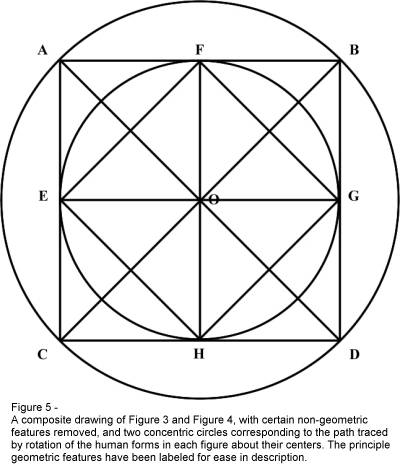
Figure 5 is a composite of Figure 3 and Figure 4, absent the human form, zodiac, and numbers and with the geometric shapes labeled to facilitate discussion. Figure 5 does however add two concentric circles to the composite. One of the two squares (ABDC) therefore appears circumscribed about the larger circle, and the other (EFGH) appears inscribed within the smaller circle. These squares are arranged such that the diagonals of square EFGH (Line FH and Line EG) are both the diameters of the circle, as well as the height and width, respectively, of square ABDC.  The multiple intersections of the diagonals of the squares and of the diagonals with the sides of the squares produce no fewer than sixteen (16) identical isosceles right triangles.

It is not especially difficult to determine the underlying geometric significance of these figures. The reader will readily be able to discern that the area of Square ABDC is twice that of Square EFGH based strictly upon the fact that the radius of the two circles are in a 2:1 ratio with respect to one another. This of course places the height of the two squares in a similar ratio, and also the area of the squares.   The consequence of this figure is then that when a square is circumscribed about a circle, its area will be twice that of a square inscribed in the same circle. The two concentric circles in Figure 6 share a similar relationship; namely, the area of the circle circumscribed about Square ABDC has twice the area of the circle inscribed in Square ABDC. This concept is summarized in Archimedes Book of Lemmas[vii], Proposition 7 in which it is stated:

“If circles are circumscribed about and inscribed in a square, the circumscribed circle is double of the inscribed square”

Proposition 7 is known to be the basis by which Archimedes approximated the value of Pi (3.14159…) using his famous method of exhaustion[viii]. This concept is also reflected by Euclid in Book XII of Elements, Proposition 1[ix].  These figures were crucial in the later discovery of (Figure 6) the mathematical properties of the lune of Hippocrates[x] (A lune is a plane figure bounded by two circular arcs of unequal radii, i.e., a crescent[xi]) by Euler in 1771[xii]. Agrippa’s figures illustrated here as well as the lune occupied a prominent position in the age old quest to “Square the Circle”. This was, of course prior to the discovery that the value of Pi was an indeterminate number.

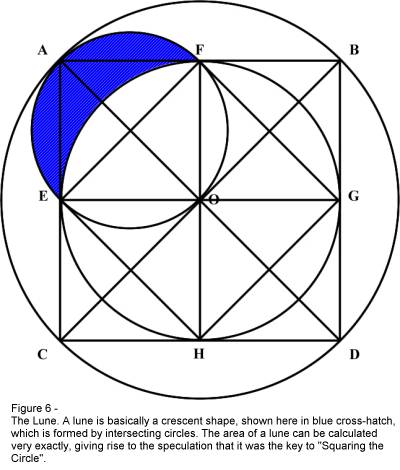
Note that in Figure 6, the Square ABDC is four times larger than is Square AFOE. The difference in the relative areas of the two squares and also of the two circles forming the lune are therefore, proportionate.

In her book The Music of Pythagoras[xiii], author Kitty Ferguson describes a scene from Plato’s Meno in which Socrates and Meno are discussing the figure of a four foot square which Socrates has drawn in the sand. It is related that during the discussion Socrates uses this square as a basis for the construction of a figure identical to that shown in Figure 5, less the circles. In the course of developing this figure, Socrates leads one of Meno’s servants in a dialog in which the servant deduces that the area of the larger square is twice that of the smaller square. The entire purpose of this scene in Meno is to illustrate that man is capable of developing knowledge by deduction, and does not rely simply upon a priori knowledge, or knowledge which is already fully developed and present at birth. No doubt, the figures later published by Agrippa included the symbolism of the ability of man to discern and to employ deductive reasoning.  However it is the Geometric not the Philosophical principles which are of interest in paper; it is notable in this respect that the two figures of interest illustrate proportional characteristics of the human form which are not directly related to the Golden Mean (Phi or the Divine Ratio). This is not the case with Leonardo’s Vitruvian Man nor is it the case with the remaining figures given by Agrippa (as shown in Figure 2).

This is not to say that the value of Phi cannot be developed using these two figures, which it clearly can (Figure 7). However the value of Phi does not coincide with distinct body features in these figures. The fact that these figures are included with a series of other sketches which clearly describe the Phi proportions of the human body would lead us to believe that Agrippa considered the geometric relationships between inscribed and circumscribed squares and circles to be sufficiently non-coincidental as to be considered evidence of the divine origin of Man.

This is of special interest to Freemasonry, since the two figures being discussed reveal absolute geometric proportions in the human form, and do not depend upon mathematical (i.e. non-geometric) principles to make this point.7

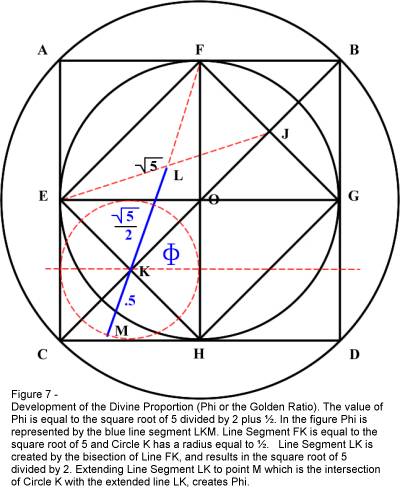
In Figure 7, consider the rectangle EFJK. If we assume that the long sides of this rectangle have a dimensional value of two (2) units, and that the short sides a dimensional value of one (1) unit, then the diagonal of this rectangle (line FK) has a value equal to the square root of five. The value of Phi is very closely associated with the square root of five, being equal to the square root of five divided by two, plus one-half (1.114213 + .5 = 1.614213).  By constructing the opposing diagonal JE, we are able to produce Point L which lies at the bisection of the two diagonals. Therefore in order to demonstrate the value of Phi in our figure, we have only to add the value of one-half unit to Line Segment LK. We accomplish this by extending line LK to Point M, which is the point at which it intersects with Circle K, which has a radius of ½. The entire line segment LKM then, has a length equal to the square root of two plus one-half, which is the value of Phi. Note that this process also results in the construction of Circle K, which is a circle inscribed within Square EOHC. The ratio of the area of Square EFGH to that of Square EOHC is 4:1; and consequently the ratio of the area of inner Circle O to that of Circle K is also 4:1. Further note that Phi may also be developed using Figure 6 as the basis, in which case the smaller circle is circumscribed about Square AFOE, and the ratio of Square AFOE and the smaller circle in Figure 6 to Square ABDC and the outer Circle O, which is circumscribed about Square ABDC is 4:1.

Heraclitus (540-480) is credited with saying “Man is the measure of all things”[xiv]. This Figure is, as are the two figures in Agrippa’s Occult Philosophy, the geometric representation of Man as a Divine creation, centered in the universe, with God-given faculties of reason, and physically formed in Divine proportion.