The numbers 3, 5, and 7 are significant in the Craft, as is evident from the dramatic manner in which these numbers are brought to the attention of a Fellowcraft Mason during the ritual of the Degree. It has always been interesting to me that beyond the literal explanation provided during that Degree, very little is presented thereafter regarding any possible metaphoric or symbolic use of this numerical progression. In fact the only memory I have of further formal reference to, or use of, the numbers 3, 5, and 7 is for certain applause cadences associated with Scottish Rite ritual.

 Since much of the symbolism of Freemasonry deals with geometry or geometric construction, it seemed reasonable to me that there may be subtle meaning contained in the numerical sequence 3, 5, and 7 which might only be brought to light by examining the numbers in a Geometrical context. As will be demonstrated, one method for the geometric representation of the numbers 3, 5, and 7 is in the form of intersecting circles . This approach produced an astonishingly simple proof of Euclid’s 47^th Proposition. It would appear that Euclid’s famous theorem pops up with surprising regularity in Freemasonry. This is perhaps no surprise since Euclid’s 47^th Proposition is regarded as foundational to the understanding of the mysteries of Freemasonry.

This paper will present a detailed account of how the numbers 3,5, and 7 when translated into a diagram of intersecting circles resulted in a proof of Euclid’s 47^th Proposition. Interestingly, I developed  this proof, then discovered through additional research that an identical proof has already been established by a 14 year old girl from Iran[i] (Miss Sina Shiehyan from Sabzevar, Iran), using an identical figure or diagram, but developed by methods which did not involve either circles or the numbers 3, 5, and 7 (talk about ego deflation). Consequently I make no claims for having originated the proof, but present it here for the sole reason that it is based upon a numerical progression and unique geometric representation which is of interest to the Craft.

Geometric Representation

During the preparation of this article, a number of different approaches were taken (including arrangements based upon The Lune of Hippocratus, and Three Co-Tangent Circles, neither of which worked), to represent the numerical progression 3, 5, and 7 in geometric form.  Of these approaches, the one which appeared most interesting to me was one in which the numbers in the sequence were made to represent circles having a diameter equal to their numerical value. I felt it was important to arrange the circles in such a manner that the progression of the numbers was maintained (i.e.  3 + 0, then 3 +2, then 5 + 2). In this progression each number increases by two relative to the sum of the two preceding numbers. It’s interesting to note that the number one (1) is not included in this sequence, even though it clearly fits into the pattern (1 + 0 = 1, 1 + 2 = 3, 3 + 2 = 5, 5 + 2 = 7). The fact that the number 1 is absent from our Masonic sequence was puzzling. One possible reason is that in a linear progression of numbers, only three are necessary to establish that the progression is indeed linear. For example, when plotting a graph, if the alignment of any three points on that graph may be connected with a common straight line, then the plotted values represented by these points are linear. 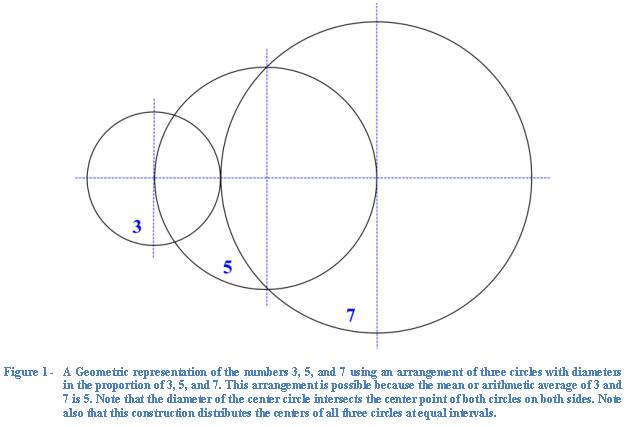The slope of the straight line connecting these points is constant at any point along it’s length. Figure 1 is the representation of the circles having proportions of 3, 5, and 7 which I have described. The progression in the diameter of each circle is represented by the method in which the circles overlap, with the constant increase in each successive diameter depicted by the uniform spacing between the circle centers. This representation also captures the fact that the numbers 3 and 7 when added total 10; and that 5 is the mathematical mean or average of the sum of these two numbers.

Development of the Figure of Proof

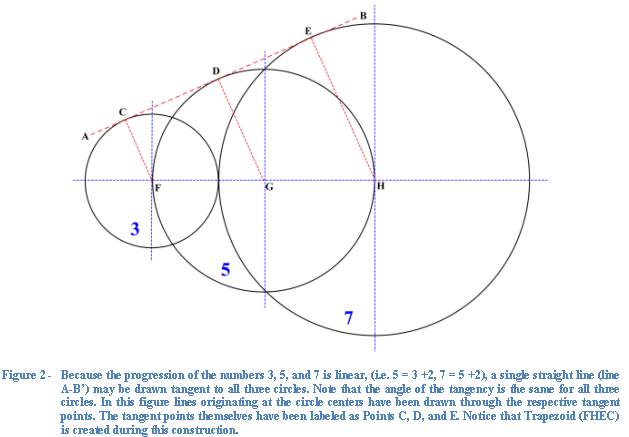
Since the relationship between the diameter of these circles is linear, I am able to construct a straight line which is simultaneously tangent to all three circles (Figure 2).  In Figure 2 the tangent line is represented by line AB. Lines have been drawn from the center of each circle (the centers are labeled as points F, G, and H) to points perpendicular to tangent line AB where it intersects each circle. These points of tangency are labeled C, D, and E respectively. Notice that all three lines are parallel to one another and that they pass through their point of tangency at the same angle. Although not shown in the figure, extension of line AB to the left of the first circle would eventually result in the tangent line intersecting the blue dotted line which depicts the common diameter and horizontal centers of the three circles. This would represent the origin or convergence point of the progression. An infinite number of circles, each successively decreasing in size, but maintaining the proportions 3, 5, and 7 (and overlapped exactly like those shown in the figure) would fit perfectly at tangent points between these two converging lines. There are many highly interesting geometric and mathematical properties represented here, however it is beyond both the scope and focus of this article to delve into these.

In Figure 3 we have constructed line DN which is perpendicular to line FH and which is also tangent to both the first circle and center circle at point N.  A right triangle (FHD) has been inscribed in the center circle (based upon the Theorem of Thales[ii] triangle FHD is a right triangle) with the vertex of the right angle at point D (the point at which AB is tangent to the center circle). This divides trapezoid FHEC into three similar right triangles FDC, HED, and FHD.  In addition, line DN divides the larger triangle FHD into two smaller right triangles, FND and HND. Note that triangles HED and HDN are congruent (identical) and that triangles FCD and FND are also congruent.

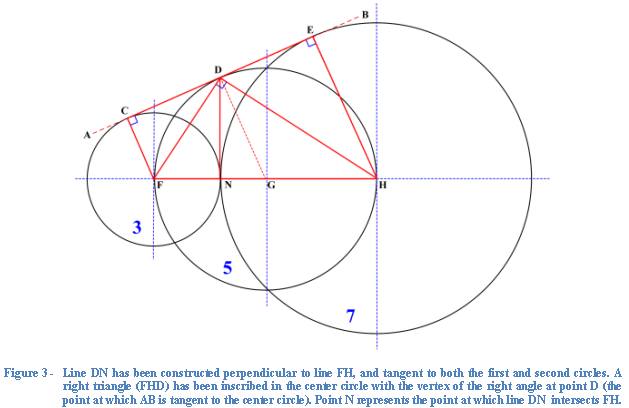
            Figure 3 provides an excellent opportunity for a glimpse of the proof. Notice that triangle FCD and triangle HED may both be “folded” down onto the triangle FHD (along lines FD and HD respectively) so that they exactly coincide with triangles FND and HED, completely filling the area represented by triangle FHD._.  This obviously means that the area of the two triangles FCD and HED when added together equal the area of the larger triangle FHD.  Therefore, we can state that two times the area of triangle FHD will equal the area of trapezoid FHEC which is composed of the three triangles. The proof is predicated upon this principle.

Demonstration of Proof

Before beginning the demonstration of proof I would like to offer a short comment concerning the Pythagorean Theorem (aka Euclid’s 47^th Proposition) which may assist some readers in understanding how and why the proof works. The Pythagorean Theorem establishes that in a right triangle the square of the length of the hypotenuse of that triangle will equal the square of the sums of the lengths of the other two sides. We state this mathematically as c² = a² + b² in which c is the hypotenuse and a and b are the other two sides. 

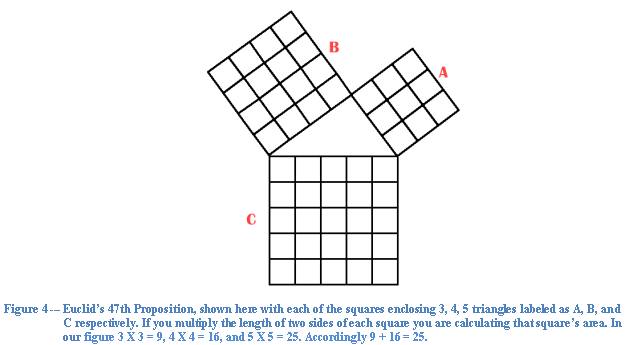
Although we identify the Pythagorean Theorem with the calculation of the length of the sides of a right triangle, its basis of proof is actually in the calculation of areas.  The Pythagorean Theorem may be rewritten to state that the sum of the area of the squares enclosing two sides of a right triangle will equal the area of the square forming the hypotenuse of that triangle.  One figure often used to establish the proof of this restated version of the Pythagorean Theorem is provided by Figure 4. Consequently, one method of proof of the Pythagorean Theorem involves demonstrating that the area of side c² in a right triangle is equal to the area of some other polygon (often a trapezoid) in which it is exactly contained. Often, several right triangles which may be summed to equal the area of a polygon are used to the same effect.

 As previously mentioned, the original proof which I developed is the same as that developed by Ms. Shiehyan, with the exception that I used slightly different algebra than she did, and my figure of proof was developed using a different premise. I will provide both the proof she developed as well as my own, in case one should happen to be more easily followed than the other (different readers will have different perceptions). The original proof offered by Ms. Shiehyan is presented in it’s entirety at the excellent internet website Cut The Knot[iii], an interactive internet mathematics website containing, among many other things, a collection of proofs of the Pythagorean Theorem. In addition to being much smarter than I am, Ms. Shiekhan has far better handwriting than I.

Refer to the diagram of proof provided by Figure 3. Note that the labeling of my figure differs from that used by Ms. Shiekhan and I have changed the lettering of the proof to coincide with the differences. Her proof of Euclid’s 47^th Proposition follows:

·        Area (FDC)  + Area (HDE)  =  DC * AP/2  +  DE * HE/2  = {BA* (FC + HE)/2}/2 =Area (FHEC)/2

·        Therefore AREA (FHD) = Area (FHEC)/2

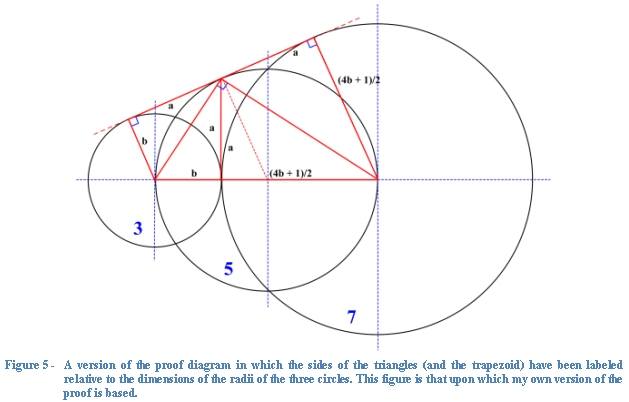
·                    My own version of the proof is a little different. In order to assist the reader in understanding my method, I have provided Figure 5, which is identical to Figure 3 in all respects except the labeling. I have used lower case letters to designate the various sides of the triangle relative to the length of the various radii of the three circles. As above I compare the summed area of the triangles to the area of the trapezoid. This method is actually more complex but provides more algebraic detail.

·         Area of the Trapezoid = {(4b + 1)/2 + ( b}/2 * 2a = (5b + 1)/2 *a = 5ab + a = 5a (b + 1)/2

·        Area of Large Triangle = Sum of the Area of the Two Smaller Triangles

·        Area of Large Triangle = ab/2 + [a*{(4b + 1)/2}]/2= [{ab/2 + (4ab + a)/2}]/2 = [{(5ab + a)/2}]/2 = [5a(b+1)/2]/2

·        Area of Trapezoid = Two Times the Large Triangle and,

·        Therefore 2 *[5a(b + 1)/2}]/2 =  5a (b + 1)/2

·        Hence the Area of the Trapezoid = Twice the Area of the Large Triangle

Significance

            The question of significance pertains to why the ability to produce a proof of Euclid’s 47^th Proposition using circles having the proportions of 3, 5, and 7 matters or is even relevant to Freemasonry.  The answer of course depends upon one’s perspective on the Craft. In my own case, the ability to produce an association with Euclid’s 47^th Proposition is a reminder that Geometry (note the capital G) is everywhere; all we have to do is look. It is also, I believe, useful to explore our long established symbols, whether those symbols be text or graphic in nature; without a thorough understanding gained by such exploration we cannot possibly say that we understand our Craft. The Fellowcraft Degree in which the numbers 3, 5, and 7 are prominent, is also that in which we are instructed to study the seven liberal sciences, one of which is Geometry.

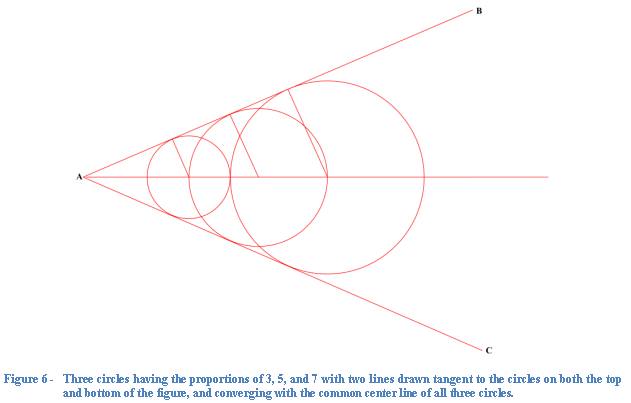
            Having said that, I would like to present an interesting situation which I discovered during the course of my research for this article.  Figure 6 below is a version of the three circles having the proportions of 3, 5, and 7 similar to that shown in Figure 2; except that in this version I have drawn two lines tangent to the circles on both as sides (lines AB and AC) and with both tangent lines and the line representing the common center of the circles converging at point A.

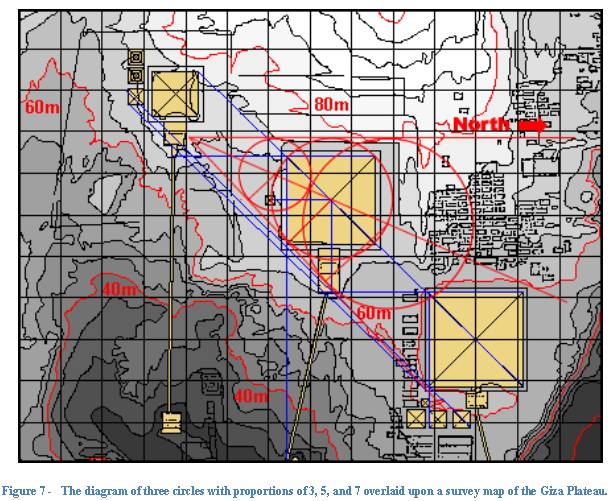
Figure 7 presents this same figure overlaid upon a survey plot[iv] of the Giza Plateau, home of the great Pyramids of Egypt. Note that when the center circle is properly aligned and positioned over the center Pyramid, both the center line and one tangent line intersect at the exact center of the structure. Note that simultaneously the other (opposite) tangent line points due North. The point of convergence falls approximately left (right to the reader) and center of the structure located just in front of the first (small) pyramid. Further examination of the figure reveals that the line from the center of the middle circle to the point of tangency coincides with the diagonal of the pyramid, and also forms one of three similar right triangles.

This is an amazing coincidence, since this use of the figure would permit alignment of the pyramid to true North and also serve to define the four corners and diagonals of the structure and locate it’s center. The third (lower structure in Figure 7) pyramid incidentally may also be aligned when the center circle and remainder of the figure are moved directly over it. The convergence point in this case coincides with the small structure in front of the middle pyramid, almost exactly duplicating the position in which it converged in the first instance. If this was the surveyor’s vantage point, as this would suggest, it may be the point where the best unobstructed view was available. When viewing this figure please take into account small inaccuracies in the construction of the scaled figure showing the three circles, tangent lines, etc. and the relatively large scale of the plateau survey.

I am not suggesting that this is proof that this was the method used to align or build the great pyramids, nor that the pyramids are connected with Freemasonry. I think any reader however would agree that the coincidence is startling. As with many of my articles, I leave it to the reader to draw his own conclusions in this matter.