|
American
Sports Figure and inadvertent wit Yogi Berra is credited with saying “If you
don’t plan where you’re going, you’ll end up someplace else”.
I frequently take exactly this sort of unplanned journey using the
internet as my vehicle. More often than not my starting place is some Masonic
concept or bit of symbolism which interests me, and on especially good journeys
I actually end up discovering things which a more rigid, planned approach would
have caused me to by-pass. The paper you are about to read is the product of
just this sort of journey.
While
performing internet based research on the symbolism of the “Point Within a
Circle”, I happened upon a link to a website which offers various mathematical
proofs of Euclid's 47th Proposition. One of these proofs
immediately caught my eye, since it had been developed by Brother James A.
Garfield, the twentieth President of the United States, and a Freemason. Bro.
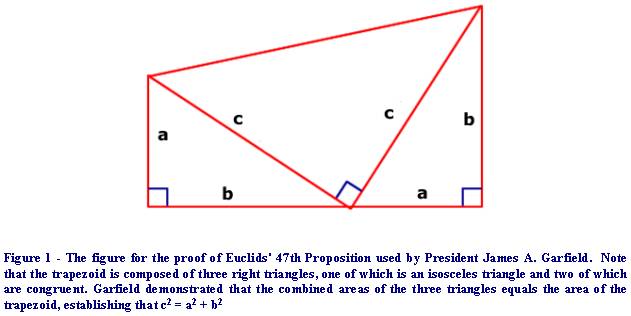
Garfields’ elegant and quite famous[i]
proof involves the construction of a trapezoid which is divided into three
separate right triangles[ii]
(Figure 1). Two of these triangles are congruent and one is an Isoceles triangle.
Garfield demonstrated through algebraic means that the area of the trapezoid is
equal to the sum of the areas of the three right triangles and thereby proved
that c2=a2 + b2. Garfields’ proof,
which I happened upon when I also had the “Point Within a Circle” symbol
fresh in my mind, led me to consider whether the figure of the “Point Within a
Circle” might be used to construct a similar or even identical proof. As will
be demonstrated, the figure of a “Point Within a Circle” can not only be
used to construct a proof of Euclid's 47th Proposition, it leads to
the exact same method in doing so as that which was published by President
Garfield.
In order to prepare the reader for this demonstration, I will present a
brief and very basic discussion concerning Euclid's 47th
Proposition. Readers with a greater interest or who may be interested in a more
complete discussion will find exhaustive reference material to this effect on
the internet. I will follow with the construction of the diagram I used to
demonstrate the proof in which the “Point Within a Circle” is a critical
element. Finally I will complete the algebraic portion of the proof using the
exact same equations and mathematical methods used by Garfield. Please note that
I do not claim this proof to be original in any way other than the fact that it
was developed using the “Point Within a Circle” as the basis for
constructing the figure or diagram upon which Garfields’ proof is based.
Euclid's
47th Proposition
During
ones’ journey through the rituals of Freemasonry, it is nearly impossible to
escape exposure to Euclid's 47th Proposition and the Masonic symbol
which depicts the proof of this amazing element of Geometry.
Euclid's 47th Proposition of course presents what we
commonly call the Pythagorean Theorem. The Pythagorean Theorem establishes that
the square of the length of the hypotenuse in a right triangle will equal the
square of the sums of the lengths of the other two sides. We state this
mathematically as c2 = a2 + b2 in which “c”
is the hypotenuse and “a” and “b” are the other two sides.
Although
we identify the Pythagorean Theorem with the calculation of the length of the
sides of a right triangle, its basis of proof is actually in the calculation of
areas. The Pythagorean Theorem may
be rephrased to state that the sum of the area of the squares enclosing two
sides of a right triangle will equal the area of the square forming the side
which is the hypotenuse of that triangle. One
figure often used to establish the proof of this restated version of the
Pythagorean Theorem is provided by Figure 2. Brilliant use is made in this
figure of the first set of the Pythagorean Triples [iii]
3, 4, and 5.

Much
is made of Euclid's 47th Proposition in Freemasonry, primarily in
the third degree of the Craft. While the value of this Proposition to an
Operative Mason is immediately apparent, its’
meaning to the Speculative Mason is somewhat less so. The assumption of many
Masons is that there is a great and abiding allusion contained within the
Theorem, but this allusion is so heavily veiled or so subtle in meaning that it
is incomprehensible. I personally continue to search for more light in
Freemasonry through research in those areas which interest me. I might add that
my efforts have never failed to deliver a greater understanding of the Craft.
I
will begin my discussion of the proof of Euclid's 47th Proposition
with the simple expedient of referring the reader to two seminal papers which
describe the method for inscribing a right triangle in a circle in accordance
with the Theorem of Thales. The first of these is contained in a paper[iv]
presented during the 222nd Anniversary of Independent Royal Arch
Lodge No. 2, F. & A.M. by Bro.
Brent Morris. A second, also very
detailed, paper[v] describing the use of this method to construct a right
triangle is given by Bro. William F. Bowe in The Builder Magazine. Both of these
articles explain Euclid's Theorems: Theorem
12, contained in Book III of Euclid's Elements[vi]
in which it is stated that “An angle
inscribed in a semi-circle is a right angle”. This Theorem is based
upon an even older Theorem to the same effect developed by Greek Philosopher,
Astronomer, and Mathematician Thales of Miletus[vii].
As
stated, my demonstration makes exclusive use of the “Point Within a Circle”
to develop the proof figure introduced by President Garfield. Accordingly my
initial step in this proof is to draw the “Point Within a Circle” as a
diagram, which I have done in Figure 3. I have added to this figure a straight
line (“AB”) across the diameter of the circle and perpendicular to the two
parallel lines (lines “CD” and “EF”) at the points at which these lines
are tangent to the circle.

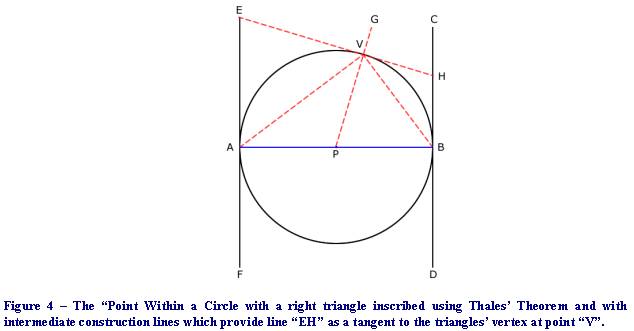
I
next use Thales’ Theorem to construct a right triangle (“ABV”) in the
semicircle. I add line “PG” which begins at the center point “P” of the
circle and which extends through the vertex of the right triangle (“point
V”). Line “EH” is then added which forms a perpendicular intersection at
point “V”, establishing itself as a line tangent to the circle at this point.
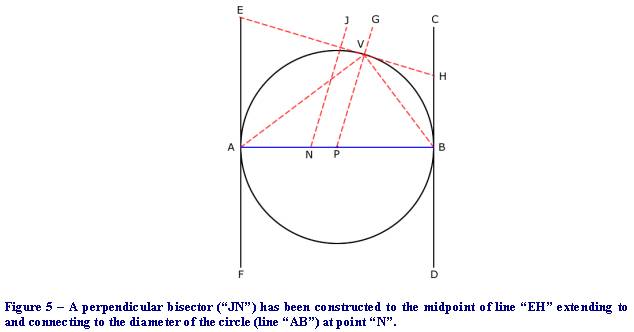
I
now construct a line (“JN”)which forms a perpendicular intersection at the
midpoint of line “EH”. Note that this line is parallel to line “PG” and
intersects the diameter line (“AB”) at point “N”. This is shown in
Figure 5.
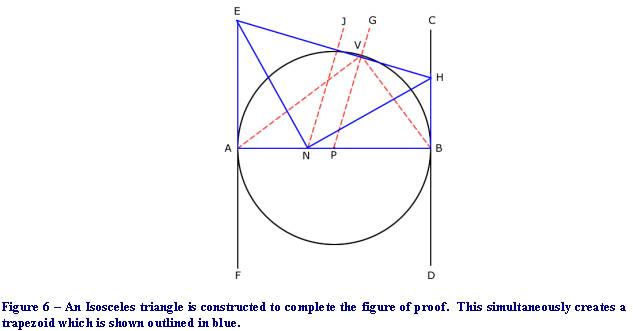
I
next use a variation of Thales’ Theorem to construct an Isosceles triangle by
joining point “N” with the points at which lines “CD” and “EF” are
intersected by line “EH”. For those who are interested in further reading
concerning this technique for creating a right triangle using a circle and
tangent lines, I refer them to an article[viii]
published in Pietre-Stones Review of Freemasonry which goes into greater detail.
Note that in constructing the isosceles triangle and the various construction
lines I have simultaneously created in this figure a trapezoid (“ABHE”) composed
of three right triangles, one of which is an isosceles triangle and two of which
are congruent. In Figure 6 the trapezoid is outlined in blue for greater
clarity.
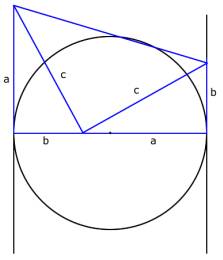
Figure
7 shows the trapezoid without the construction lines and extraneous labels. I
have labeled the bases (“a” and “b”) of the trapezoid, and the
hypotenuses of the two right triangles (“c”). Note that the figure is nearly
identical to that used by Bro. Garfield; although I have constructed the figure
at hand with the slope of the trapezoid downhill. An uphill slope (making the
figure truly identical to Garfields’) would have simply required construction
of the Thales Triangle using a point left of center as the vertex. Incidentally
Bro. Garfield was left-handed[ix].
Using
this proof figure and the associated labels I apply the exact same algebraic
sequence for developing the proof as was applied by Bro. Garfield:

Whether
the President was ever aware that the Masonic symbol of the “Point Within a
Circle” could be used to prove Euclid's 47th Proposition in a
manner so nearly identical to that which he demonstrated is of course unknown.
It does however stir the imagination. President Garfield was, during his
lifetime, a teacher of mathematics with a deep and abiding interest in Geometry
(else there would likely be no Garfields’ Proof).
As mentioned he was also a Freemason and would have been acquainted with
the “Point Within a Circle”. I
leave it to the reader to decide for himself whether Garfields’ proof was
inspired by Masonic symbolism.
[ii]
Pappas, T. "The Pythagorean Theorem,"
"A Twist to the Pythagorean Theorem," and "The Pythagorean
Theorem and President Garfield." The
Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 4, 30,
and 200-201, 1989.
[iii]
Pythagorean triples are sets of three integers which satisfy the condition c2=a2+b2.
[iv]
Morris, Brent S. The Hidden
Secrets of a Master Mason – A Speculation on Unrecognized Operative Secrets
in Modern Masonic Ritual. 1982. http://www.mn-masons.org/assets/2368.pdf.
Accessed May 28, 2007.
[v]Bowe,William
F. A Certain Point Within a Circle. The Builder Magazine, vol. 4, no. 7
(1918).
[vi]
Joyce, D.E., Euclid’s Elements, Clark University. (1996, 1997, 1998).
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html Accessed April
29, 2007.
[vii]
O’Grady, Patricia. “Thales of Miletus”. The Internet Encyclopedia of
Philosophy, http://www.iep.utm.edu/, Accessed May 1, 2007
|
![]() News Feed |
News Feed |  Subscribe News by Email
Subscribe News by Email