© All editorial matter contained in this Magazine is copyright and may not reproduced without written permission from the publisher

WE HEAR A LOT about the 'mysteries' of ancient operative stonemasons. Did they really have any that we can prove? The answer is yes -as did most trades and professions. Remember, in those days your job was everything. There were no social benefits if you were out of work; you and your family starved. If there were any special skills or tricks of your trade, you guarded them jealously because you would invariably have served an apprenticeship of several years before you became fully qualified. These were the real mysteries. 

First of all, let me say that the 'mysteries' word has been blown up out of all proportion in the masonic field. The word 'mestiere' in Italian means 'trade' or 'craft' - and the word is similar in French and, most importantly, Latin. When Anglo-Saxon ears heard the word, they immediately equated it with 'mystery' -and as everyone loves a mystery, a 'great secret' was born! 

So what were the secrets of the trade that the operative masons kept from cowans? If you were a stonemason, apart from the skill of preparing stone -which could only be obtained through lots of experience -there were easily-understood tips or secrets which they kept among themselves as a means of protecting their trade. Other trades did the same. 

If you are creating a building, there were still are -three basic essentials: the building must be level; perfectly upright; and square (at the corners, that is). DIY enthusiasts who build even small structures, will tell you that if you don't get the corners really square, the whole building will start to spiral. Perhaps not much ofa problem with, say, a garage, but wjthchurch or castle, some strange shapes can occur. 

The Basics 

The level is an obvious one. As is the plumb line. At one time a workman discovered that if you tie a length of string to a pebble and hang it, the 'line' it draws in the air will be perfectly upright.

 But a right-angled corner is more difficult. The operatives would have had a large, wooden triangular right-angled frame, from which the stonemasons could work at each corner. But because wood warps and wears, the frame had to be checked regularly. How did they make a right-angled frame in the first place? And how did they check it? 

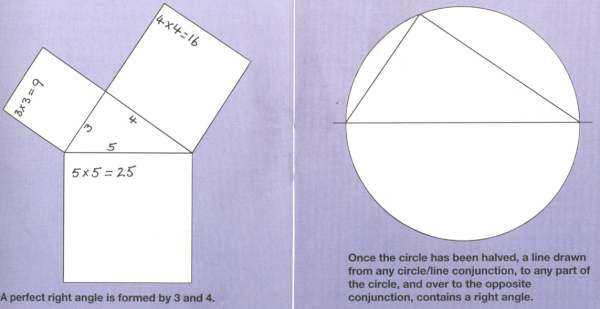
It is easy to delineate such a corner on paper. As R.J. Hollins mentions in volume two of his A Daily Advancement in Masonic Knowledge {reviewed in the last issue): With compasses, you draw a circle. Then draw a straight line through the middle of the circle passing through the centre point {which you will have made with the compasses). Youthen mark a spot anywhere on the circumference, and draw two lines from that point on the circumference, to each end of the line passing through the centre point. One of the corners of the triangle in the circle will be a perfect right angle. Easy! 

In fact, some writers have suggested that this method is the source of the original 'point within a circle'. 

Not so Easy 

But things are not that simple. It's one thing to delineate a square on paper, but how do you transpose that square to the frame necessary for the corner of a large building; a frame which should have sides several metres in length? 

The answer, believe it or not, can be found on every Past Master's collar jewel. Just below the square, you can see a curious shape which looks like an odd 'Y' consisting of three differently sized squares. This is known in the Craft as Euclid's 47th Theorem -although, to be quite honest, I think it was first propounded by Pythagoras, and he probably got it from the Chinese. 

I have a (no doubt annoying) habit of asking Past Masters what that curious 'Y' is; most of them haven't a clue, and even out of those who answer "Euclid's 47th Theorem" (only a half-dozen to date), have no idea how it works. Which just goes to show that our masonic education, such as it is, is dire. 

The actual theorem states that 'In every right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides', DON'T PANIC. What this means in English is: that the longest side of the triangle, squared, is equal to the squares of the other two sides. 

If you think this isn't much help, you can guess that it didn't much help the medieval stone masons either. In fact there are several measurements that will fit this description; what was needed, was a set of measurements that the stone masons could easily remember. Someone, somewhere, using Euclid's Theorem, noticed that in one answer, the three sides of the triangle could be in units of three, four and five. So the square of the hypotenuse (five) multiplied by itself is 25. Then 3x3 is nine and 4x4 is sixteen -and 9+ 16 is 25! Thus was born the 'secret' or mystery of the rule of 3-4-5. 

This meant that any operative mason, using any form of unit -say the length of his elbow to the tip of his fingers -could cut three lengths of timber into three, four and five units, and lay the lengths out as a triangle. The corner of the three and four, then, would be a right angle. 

This procedure is so simple, that it is obvious why operative stone masons would want to keep it secret from prying eyes. Add to that the string-and-pebble for a vertical line, and other tricks of the trade, picked up during an apprenticeship, and the stone mason had a trade at his fingertips. But the secrets, or tips, could easily be passed on by word of mouth - so it is understandable why dire threats were made, and no doubt carried out, to anyone who illegally gave the secrets to someone who had not passed along and thorough apprenticeship. 

What the freemasons have made of those secrets or mysteries, is another story.